蜗轮强度校验
蜗轮齿面的接触应力强度计算
蜗轮齿面的接触应力强度计算是确保蜗杆传动可靠性的关键环节，其核心是验算最大接触应力是否小于材料的许用接触应力。下面为你详细解析计算公式、参数含义以及应用方法。
接触应力校核公式
蜗轮齿面接触疲劳强度的校核公式为：
$$\sigma_H = Z_E Z_\rho \sqrt{\frac{K A K_T T_2}{a^3}} \leq [\sigma]_H$$
其中：
- (\sigma_H)：蜗轮齿面的计算接触应力 (MPa)
- ([\sigma]_H)：蜗轮材料的许用接触应力 (MPa)
- (Z_E)：材料的弹性影响系数 (\sqrt{MPa})。取决于蜗杆和蜗轮的材料组合，常见配对如下：
- 钢制蜗杆 + 铸锡青铜蜗轮（ZCuSn10P1等）：(Z_E = 150 - 160 \sqrt{MPa})
- 钢制蜗杆 + 铸铝铁青铜蜗轮 (ZCuAl10Fe3) 或灰铸铁蜗轮：(Z_E = 160 \sqrt{MPa})
- (Z_\rho)：接触系数。这是一个与蜗杆传动的接触线长度和齿面综合曲率半径相关的系数，通常需要根据 (d_1 / a)（蜗杆分度圆直径与中心距的比值）查阅专门的图表或手册确定。
- (K)：载荷系数。用以考虑实际工况下的动载荷和载荷分布不均的影响，(K = K_A K_\beta K_v)。
- (K_A)：使用系数，与工作机的载荷特性有关。
- (K_\beta)：齿向载荷分布系数。
- (K_v)：动载系数。
- (A)：应用系数，通常取1.1-1.4，冲击、振动大或环境温度高时取大值。
- (T_2)：蜗轮轴上的工作转矩 (N·m)
- (a)：蜗杆传动的中心距 (mm)
- (K_T)：温度系数，考虑工作温度对润滑和材料性能的影响，需根据具体工况确定。
许用接触应力 ([\sigma]_H) 的确定
许用接触应力的确定与蜗轮材料密切相关，主要分为两种情况：
蜗轮材料为铸锡青铜（如ZCuSn10P1, ZCuSn5Pb5Zn5）：这类材料强度极限通常低于300 MPa，主要失效形式是点蚀。其许用应力与应力循环次数有关，计算公式为：
$$[\sigma]_H = K_{HN} [\sigma]_{H'}$$
其中，([\sigma]_{H'}) 是基本许用接触应力，可查表获得；(K_{HN}) 是接触强度的寿命系数，(K_{HN} = \sqrt[8]{10^7 / N})，(N) 为应力循环次数。蜗轮材料为铸铝铁青铜（如ZCuAl10Fe3）或灰铸铁（如HT200, HT150）：这类材料强度较高，主要失效形式是胶合。由于胶合不属于疲劳失效，其许用应力 ([\sigma]_H) 与循环次数 (N) 无关，可直接根据配对蜗杆的齿面硬度和预期的滑动速度 (v_s) 查表确定。
下表列出了一些常见材料组合在特定条件下的许用接触应力参考值：
| 蜗轮材料 | 铸造方法 | 蜗杆齿面硬度 | 许用接触应力 ([\sigma]_H) (MPa) 参考值 | 失效形式 | 是否与循环次数N有关 |
|---|---|---|---|---|---|
| ZCuSn10P1 （铸锡磷青铜） | 砂型（或金属型） | ≤45HRC >45HRC | 砂型150-180 金属型220-268 | 点蚀 | 是 ((K_{HN} = \sqrt[8]{10^7/N})) |
| ZCuSn5Pb5Zn5 （铸锡锌铅青铜） | 砂型（或金属型） | ≤45HRC >45HRC | 砂型113-135 金属型128-140 | 点蚀 | 是 ((K_{HN} = \sqrt[8]{10^7/N})) |
| ZCuAl10Fe3 （铸铝铁青铜） | - | >45HRC （滑动速度 (v_s=2m/s)） | 210 | 胶合 | 否（直接查表，值与(v_s)相关） |
| HT200 （灰铸铁） | - | >45HRC（滑动速度 (v_s=0.25m/s)） | 202 | 胶合 | 否（直接查表，值与(v_s)相关） |
设计公式
在初步设计时，常根据所需传递的功率和转矩，由接触强度条件初步估算中心距 (a)：
$$a \geq \sqrt[3]{K A K_T T_2 \left( \frac{Z_E Z_\rho}{[\sigma]_H} \right)^2 }$$
求得中心距 (a) 后，可据此初步选择模数 (m)、蜗杆分度圆直径 (d_1) 等参数，然后再进行精确的校核。
核心要点与选材建议
计算接触应力强度的核心是验证工作应力不超过许用应力。材料的选择直接关系到许用应力的确定方法和传动的承载能力。对于重载、要求高可靠性的闭式传动，优先选择铸锡青铜（如ZCuSn10P1）并校核点蚀强度；对于速度较高或中载且考虑成本的场合，可选用铸铝铁青铜（如ZCuAl10Fe3）并按抗胶合能力查取许用应力。
蜗轮齿根弯曲应力的校核计算
蜗轮齿根弯曲应力强度的计算是确保传动可靠性的关键一环，尤其在特定工况下尤为重要。下面为您梳理其核心计算公式、关键参数以及应用要点。
核心计算公式
蜗轮齿根弯曲疲劳强度的校核公式如下，其目的是验证计算弯曲应力是否小于材料的许用弯曲应力：
$$\sigma_F = \frac{1.53 K T_2}{d_1 d_2 m} Y_{Fa2} Y_\beta \leq [\sigma_F]$$
其中：
- (\sigma_F) 是蜗轮齿根的计算弯曲应力 (MPa)
- ([\sigma_F]) 是蜗轮材料的许用弯曲应力 (MPa)
如果需要进行初步设计来确定模数 (m)，可以使用以下设计公式：
$$m \geq \sqrt[3]{\frac{1.53 K T_2}{z_2 [\sigma_F]} Y_{Fa2} Y_\beta}$$
公式参数详解
为了正确使用公式，理解每个参数的物理意义和获取方法至关重要。下表提供了各参数的详细说明。
| 参数符号 | 参数名称 | 含义与确定方法 |
|---|---|---|
| (K) | 载荷系数 | 综合了使用情况、动载荷和齿向载荷分布的影响，(K = K_A K_V K_\beta)。其中 (K_A) 为使用系数，与工作机的载荷特性有关；(K_V) 为动载系数；(K_\beta) 为齿向载荷分布系数。 |
| (T_2) | 蜗轮上的工作转矩 | 单位通常为牛顿·米 (N·m)，是计算的原始依据。 |
| (d_1, d_2) | 分度圆直径 | 分别为蜗杆和蜗轮的分度圆直径 (mm)，是传动的基本几何参数。(d_2 = m z_2)。 |
| (m) | 模数 | 蜗杆的轴向模数（也是蜗轮的端面模数），为标准值 (mm)，决定了轮齿的大小。 |
| (Y_{Fa2}) | 齿形系数 | 这是一个重要的几何系数，反映了蜗轮轮齿的独特形状对弯曲应力的影响。它需要根据蜗轮的当量齿数 (z_{v2} = z_2 / \cos^3 \gamma) 来查表或专用图表确定。 切勿直接使用蜗轮的实际齿数。 |
| (Y_\beta) | 螺旋角影响系数 | 考虑蜗杆分度圆导程角 (\gamma) 对弯曲强度的影响。常用的计算公式为 (Y_\beta = 1 - \gamma / 140^\circ)。 |
| ([\sigma_F]) | 许用弯曲应力 | 并非材料常数，需通过 ([\sigma_F] = [\sigma_{0F}] \cdot Y_N) 计算。其中 ([\sigma_{0F}]) 是材料的基本许用弯曲应力（查表获得），(Y_N) 是考虑设计寿命的寿命系数，(Y_N = \sqrt[9]{10^6 / N})，(N) 为应力循环次数。 |
主要应用场景与重要性
在下列情况下，进行蜗轮齿根弯曲强度计算尤为重要：
- 开式蜗杆传动：其主要失效形式是齿面磨损和轮齿弯断，因此常以弯曲强度作为主要设计准则。
- 齿数较多的蜗轮（通常 (z_2 > 90)）：细长的轮齿更易发生弯曲疲劳破坏。
- 重载动力蜗杆副：即使是在闭式传动中，也必须进行弯曲强度校核。因为过大的弯曲变形会影响传动的运动平稳性精度，而弯曲强度计算是控制变形的关键手段。
重要提示：由于蜗轮齿形复杂，要精确计算齿根弯曲应力比较困难，因此目前的计算方法是一种条件性的近似估算，通常将蜗轮近似当作斜齿圆柱齿轮来考虑。但需要特别注意，蜗轮轮齿的弯曲疲劳强度通常高于参数相近的斜齿轮，有资料指出约高40%。
基本计算流程建议
- 确定载荷与工况：明确工作转矩 (T_2)、载荷性质（以选择 (K_A)）、总工作时间（以计算循环次数 (N)）。
- 获取几何参数：根据已确定的传动方案，获取 (z_2), (\gamma) 等基本参数。
- 确定相关系数：计算当量齿数 (z_{v2}) 并据此查取齿形系数 (Y_{Fa2})；根据导程角 (\gamma) 计算 (Y_\beta)；根据工况确定载荷系数 (K)。
- 确定许用应力：根据蜗轮材料和寿命要求，确定 ([\sigma_{0F}]) 和 (Y_N)，计算得到 ([\sigma_F])。
- 代入校核：将全部参数代入校核公式进行计算，并判断是否满足 (\sigma_F \leq [\sigma_F]) 的强度条件。
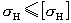和
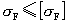，否则校验失败，须重新进行前面的参数设计。
