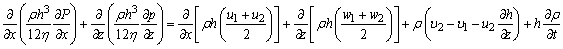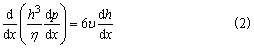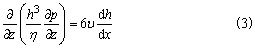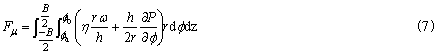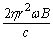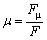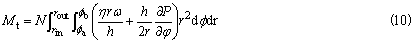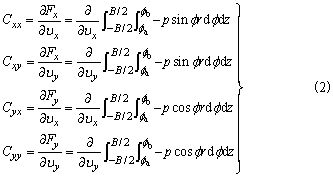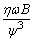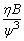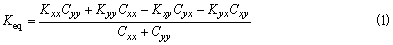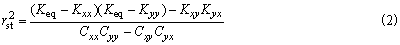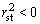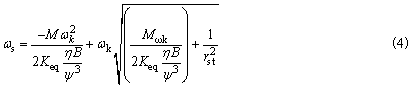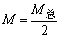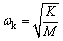液体动压润滑轴承

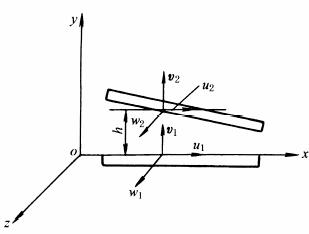
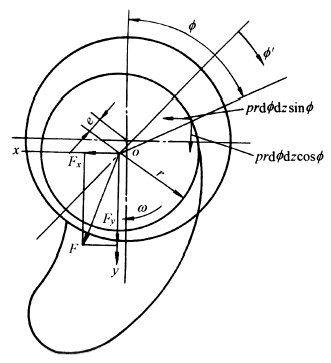
轴承的流体动压润滑微分方程(如图所示)为

                (1)

式中   η为润滑流体动力粘度，ρ为流体的密度，h为任意点油膜厚度

通常在液体润滑情况下可假定流体密度不变，为了定性分析，求出解析解，从而将上式进行简化。在稳定工况下，当轴瓦固定而轴运动时的速度为υ时，方程(1)可简化为：

按无限宽假设得

径向轴承按无限窄假设得

式(2)和式(3)的解分别见表无限宽径向轴承性能计算和表无限窄径向轴承性能计算。运用现代数值计算技术可求得式(1)的较为准确的数值解

求解式(1)、式(2)或式(3)，可得轴承内的流体压力分布p

(1)承载能力

径向轴承(图结构简图)承载力有两个分量，其中

式中  r为轴颈半径；z为轴向坐标；Φ_a、Φ_b分别为轴瓦的起始及终止处的角度；B为轴承的宽度

总承载力

推力轴承

式中    N为推力轴承的瓦块数；r_in、r_out分别是推力瓦块的内半径和外半径；Φ_a、Φ_b分别是推力瓦块的起始终止处的角度。轴承的承载能力常采用无量纲轴承特性数C_p来表示，即径向轴承

式中    ψ为轴承的间隙比，即ψ＝c/r；c为轴承的半径间隙；r为轴径半径；ω为轴颈的转速；p_m为轴承上的平均压强，p_m＝F/BD；D为轴承直径

推力轴承

式中   h_z为支点处的润滑膜厚度；B为轴瓦宽度即B＝r_out-r_in

(2)摩擦阻力和功耗

1)摩擦阻力

径向轴承轴颈上的摩擦阻力

取摩擦阻力的相对单位为，及摩擦因数，则摩擦特性系数为

C_μ＝μ/ψ或F_μ＝C_μFψ　　　　　　　　　　      　　(8)

C_μ可分为承载区摩擦特性数C_p和非承载区摩擦特性数C_t两部分，即

C_μ＝C_p+C_t　　　　　　    　　　　　　　　　　　(9)

推力轴承推力盘上的摩擦力矩

2)功耗

径向轴承

N＝F_μrω/1000　　　      　　　　　　　　　　　　(11)

推力轴承

N＝M_tω/1000　　　         　　　　　　　　　　　 　　(12)

(3)流量

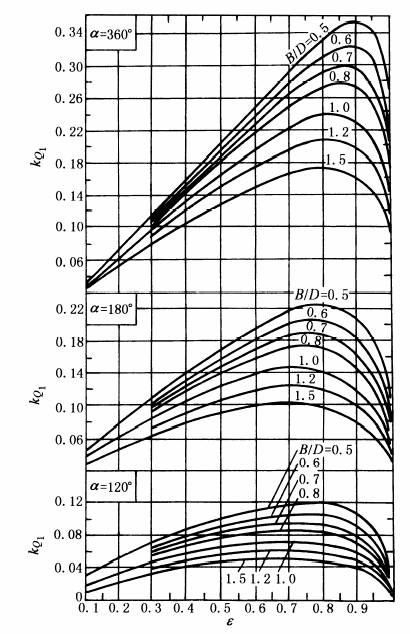
进入轴承的总流量

Q＝Q₁+Q₂+Q₃＝2(k_Q1+k_Q2+k_Q3)ψr²ωB                         (13)

式中　　 　Q₁—— 承载区端泄流量；

Q₂—— 非承载区端泄流量；

Q₃—— 轴瓦供油槽两端由供油压力产生的附加流量；

k_Q1、k_Q2、k_Q3—— 相应的流量系数

对于径向轴承，k_Q1的值参见图k_Q端泄流量系数k_Q1值

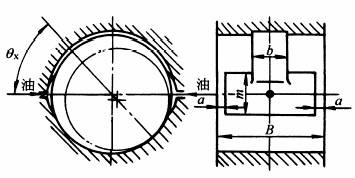
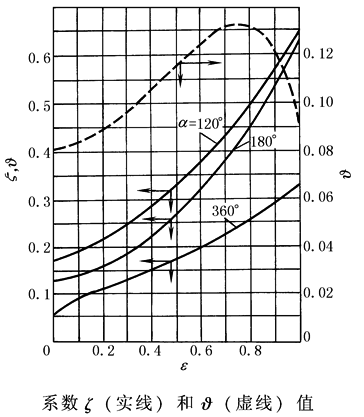
式中   p_s为供油压强；D为轴承直径；b为周向油膜槽宽，见图供油槽结构；系数ζ可由图系数ζ和θ值查出

在轴瓦水平对称布置两个供油槽(图供油槽结构)时

系数θ值由图系数ζ和θ值

在轴瓦只有一个供油槽时

h＝c(1+εcosθ_x)

式中    θ_x是供油槽中线的角坐标，从轴颈与轴承的连心线沿转动方向量起，见图供油槽结构；c为轴承半径间隙c＝rψ

(4)温升

设摩擦产生的热量全部由润滑油带走，且进油温度为t_in，端泄油的平均温度为t_m，则温升

Δt＝t_m-t_in　　　　　　　　　　　　　　　　　       (17)

1)压力供油(矿物油)轴承，温升

2)无压力供油轴承，温升

式中    E是与金属传热及润滑油比热有关的系数。轻型结构、传热困难的轴承E＝0.0091；中型及一般散热条件下的轴承E＝0.0145；强制冷却的重型轴承E＝0.0254

油膜刚度

油膜阻尼

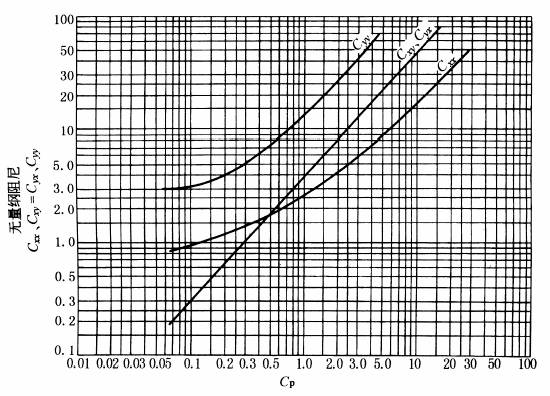
如取为油膜刚度的相对单位，为油膜阻尼的相对单位，c为轴承的半径间隙，cω为υ_x、υ_y的相对单位，则可得到相应的无量纲油膜刚度及阻尼，即K_xx、K_xy、K_yx、K_yy、C_xx、C_xy、C_yx、C_yy

以上性能计算公式均是指单瓦，如轴承为多瓦则相应轴承的性能为诸瓦之和

图圆轴承(B/D＝0.8)的C_p-K曲线和图圆轴承(B/D＝0.8)的C_p-C曲线给出了长径比B/D＝0.8时圆轴承的无量纲刚度及阻尼K_xx、K_xy、K_yx、K_yy和C_xx、C_xy、C_yx、C_yy