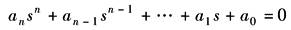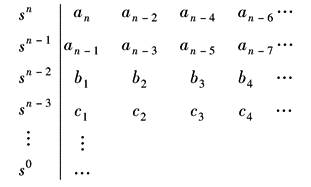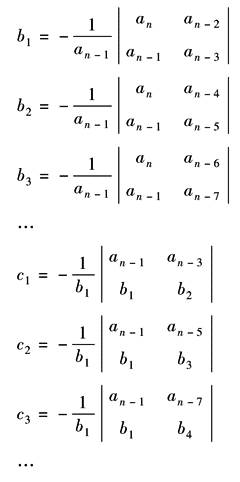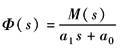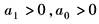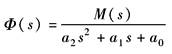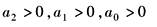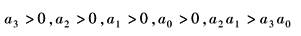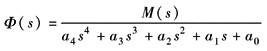线性反馈控制系统分析

(1)定义

当扰动作用消失后，控制系统能自动地由初始偏差状态恢复到原来的平衡状态，则此系统是稳定的，否则此系统是不稳定的

如果初始偏差在一定的限度内，系统才能保持稳定，初始偏差超出某一限值时，系统就不稳定，则称系统是小范围内稳定的。如果不论初始偏差多大，系统总是稳定的，则称系统是大范围稳定的。线性系统若在小范围内是稳定的，则一定也是大范围内稳定。非线性系统则可能存在小范围内稳定而大范围不稳定的情况

稳定性是控制系统重要性能指标之一，是系统正常工作的首要条件

(2)稳定的充要条件

线性反馈控制系统稳定的充要条件是它的特征方程的根均具有负实部，或者说系统的闭环极点均位于复平面的左半部

稳定性准则是分析控制系统是否稳定的依据，又称为稳定判据。工程中常用的判别系统稳定性的准则有劳斯(Routh)稳定判据和奈魁斯特(Nyquist)稳定判据

(1)劳斯稳定判据

劳斯稳定判据是一种代数准则，它利用系统的特征方程的系数来判据系统是否稳定。设系统的特征方程为

劳斯判据将方程的系数a_n，a_n-1，…，a₁，a₀列入劳斯表并计算表内元素b₁…，c₁…，…的值如下

其中

表中各行元素均计算到全部为零为止

劳斯判据：若表中第一列元素(a_n，a_n-1，b₁，c₁，…)不为零且均为正，则系统稳定；否则，系统不稳定。第一列元素符号改变的次数表示系统的特征方程根中不稳定根的数目

四阶以下系统劳斯稳定判据可以简化如下表所示

低阶系统劳斯稳定判据

阶次

系统闭环传递函数

稳定的充要条件

1

2

3

4

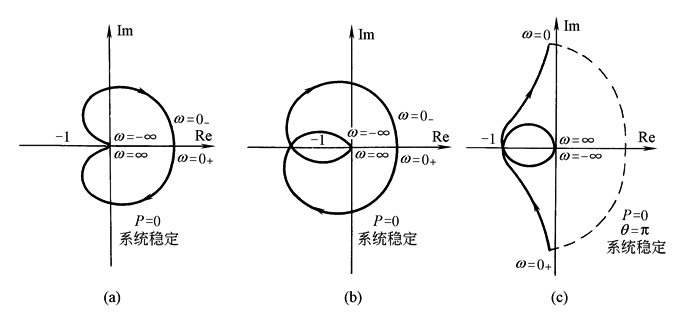
劳斯表中元素计算时，可能会出现第一列为零元素或全零行的情况，此时劳斯表的计算需参阅专门文献

(2)奈魁斯特稳定判据

奈魁斯特稳定判据是一种频率准则，它利用系统的开环频率特性来判别闭环系统是否稳定。奈魁斯特稳定判据如下：

①若系统的开环传递函数没有正实部的极点(P＝0)，当频率ω由-∞变化到∞时，开环频率特性G_k(jω)不包围复平面上的(-1，j0)点则系统稳定，否则系统不稳定；

②若系统的开环传递函数有P个极点具有正实部，当频率ω由-∞变化到∞时开环频率特性G_k(jω)逆时针方向包围(-1，j0)点P圈时系统稳定，否则系统不稳定

奈魁斯特稳定判据如图1所示，其中辅助曲线是从ω＝0_-开始顺时针方向到ω＝0₊所划的一条半径为无限大的圆周线。圆周线转角等于开环传递函数中所含的积分环节个数ν乘以π，即θ＝νπ

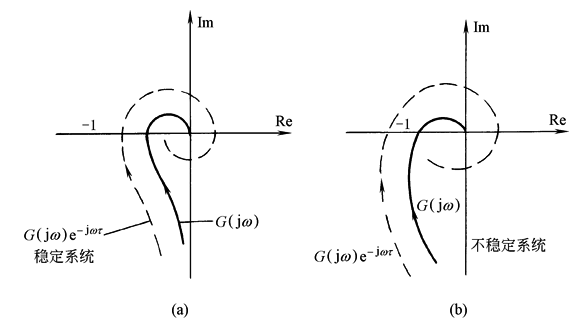
图1  奈魁斯特稳定判据

③含有延迟环节的控制系统的奈魁斯特稳定性判据为：若除延迟环节外，开环传递函数中不包含正实部的极点，闭环状态下系统稳定的充要条件是其开环频率特性G_k(jω)不包围(-1，j0)点，则系统是稳定的，如图2a所示；否则系统不稳定，如图2b所示

图2  具有延迟环节的系统稳定性判据[G_k(jω)＝G(jω)e^-jτω]

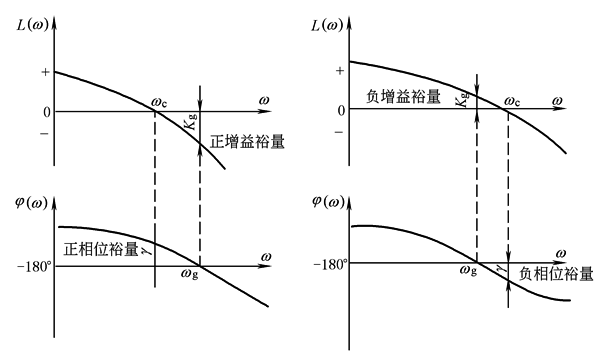
稳定裕量是衡量一个闭环控制系统相对稳定性的定量指标。在频率准则中稳定裕量通常用相位裕量γ和增益裕量K_g来表示。它们可以根据系统的开环对数频率特性来求取，其物理含义是相位迟后多少度，或开环增益增大多少倍，则系统将从稳定状态变为临界稳定状态

(1)相位裕量γ

在开环对数频率特性图上，幅频特性的增益L＝0处的相位φ(ω_c)和180°之和，即

γ＝180°+φ(ω_c)

式中，ω_c称为增益交界频率或穿越频率。γ＞0为正相位裕量，γ＜0为负相位裕量

(2)增益裕量K_g

在开环对数频率图上，相频特性φ(ω₁)＝-180°时，对应的幅频特性增益L(ω₁)的相反数，即

K_g＝-L(ω₁)

式中，ω₁称为相位交界频率。K_g＞0为正增益裕量，K_g＜0为负增益裕量

稳定裕量的含义和求取方法如下图所示

对于最小相位系统，当γ＞0、K_g＞0时系统是稳定的。一般来讲，只用单一的相位裕量或增益裕量是不足以充分说明系统的相对稳定程度的，必须同时考虑两个量。工程实际中通常要求相位裕量γ为30°~60°，对数幅频特性在增益交界频率ω_c处的斜率为-20dB/dec

稳定裕量的定义