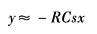控制系统的仿真

在进行自动控制系统的分析、综合和设计的过程中，除了运用理论方法对系统进行分析外，常需要进行实验研究。系统仿真就是在系统的数学模型基础上，利用计算机进行系统实验研究的一种方法

模拟仿真和数字仿真

根据仿真时所运用的计算机类型不同，仿真可分为模拟仿真、数字仿真、数字-模拟混合仿真和微机列阵组成的全数字式仿真

(1)模拟仿真

模拟仿真是以模拟计算机为主要工具，对系统的模型进行运算和研究。模拟计算机是一种在相似原理的基础上由电子元件构成的各类运算器所组成的运算装置。运算器如表1所示，各运算器的图示符号如表2所示

表1　　　　　　　　　　　　　　　　　　　　　　　各类运算器原理

一般电路组成的运算器

用直流放大器组成的运算器

y＝ax

固定位置a

表2　　　　　　　　　　　　　　　　　　　　　　　运算器图示符号

名称

符号

输出输入的关系

说明

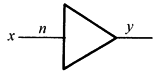
系数器

y＝-nx

完成对输入信号乘一系数n的运算，并变换正负号。一般n是整数1~20。n＝1时，只完成正负号变换

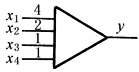
加法器

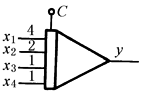
y＝-(4x₁+2x₂+x₃+x₄)

完成输入信号乘以数后的加法运算

x₁、x₂、x₃、x₄是输入信号，4、2、1、1表示对应的应乘的系数

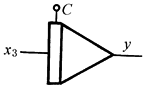
积分器

y＝-3∫xdt+C

完成输入信号乘以一定系数后的积分运算

C是初始条件值加入端

3是应乘的系数

积分加法器

y＝-∫(4x₁+2x₂+x₃+x₄)dt+C

完成各输入信号乘以一定系数后相加，再进行积分的运算

C是初始条件值加入端

系数电位计

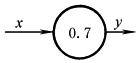
y＝0.7x

完成小于1的非整数系数设定运算

乘法器

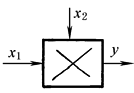
y＝x₁x₂

完成输入信号相乘运算

函数发生器

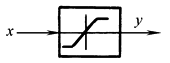
y＝f(x)

完成非线性函数的运算

模拟仿真的大致步骤是：首先将物理系统的数学模型转化为模拟计算机的电路原理图，然后选择幅值比例尺、时间比例尺和运算器的系数值，通过排题板排题，静态和动态检查，最后进行仿真运算并输出仿真结果

(2)数字仿真

数字仿真是以数字计算机为主要工具，基于数值计算的原理对系统的数学模型进行数值求解，以实现对系统分析和研究。数字仿真的过程大致为：

① 建立物理系统的数学模型，如微分方程、传递函数或方块图以及状态方程；

② 建立仿真模型，所谓仿真模型是指数字计算能运算的离散化数学模型，如差分方程等，仿真模型通常有数值计算方法中的欧拉法和龙格-库塔法等以及近代计算方法中的图斯汀法、离散相似法和状态转移法等；

③ 编制仿真程序；

④ 上机操作，进行仿真实验；

⑤ 输出仿真结果

仿真技术的应用

仿真技术在控制系统分析和设计中的应用主要是：

① 对系统的性能进行分析，验证新设计系统的可行性；

② 根据对系统的性能要求，确定控制器的结构和参数，并进行优化；

③ 进行系统模型的辨识

另外，仿真技术是实现控制系统计算机辅助设计和建立仿真器的基础，也可推广运用到系统性能预测和系统故障分析等方面

本节主要介绍离散相似法数字仿真方法，模拟仿真和其他数字仿真方法可参阅专门文献。