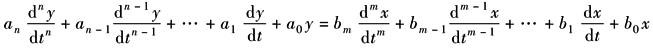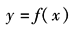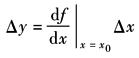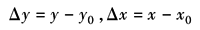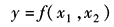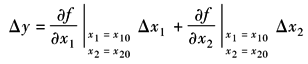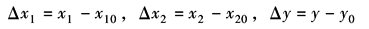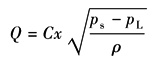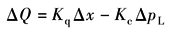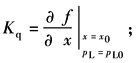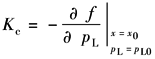微分方程
微分方程
|
微分方程 |
|---|
|
控制系统的运动特性可用一定形式的数学式来描述,通常称为系统的数学模型。在自动控制系统的分析和设计中,建立一个合理的数学模型是一项极为重要的任务。系统的数学模型可用解析法和实验法来建立。解析法是从元件或系统所依据的物理规律出发,从理论上推导出输入输出变量及内部变量之间的数学关系式。实验法是对实际系统输入一个一定形式的输入信号,根据实测的输出响应来建立系统的数学模型 经典控制理论中描述线性控制系统的数学模型有微分方程、传递函数、函数方块图、信号流图、脉冲响应函数、阶跃响应函数和频率特性等。一个系统当采用不同的方法来分析和设计时将用到不同的数学模型 (1)线性微分方程 线性元件或线性定常连续系统运动特性的数学方程是常系数线性微分方程,其一般形式为
式中 x——元件或系统的输入量; y——元件或系统的输出量; an、…、a0,bm、…、b0——由系统的结构参数决定的常系数,实际的系统,均满足m≤n的条件 (2)非线性运动方程的线性化 实际的自动控制系统中经常存在一些非线性因素,液压伺服系统中通过阀的流量特性就是非线性方程。当研究在某一工作点附近的运动特性或所研究的系统变量在动态过程中偏离平衡点不大时,可以应用线性化的方法把非线性运动方程转化为线性微分方程,称为非线性方程的线性化。线性化的目的是使某些非线性问题近似为线性问题。线性化的数学方法是将非线性函数在某工作点展开成泰勒级数后,取其一阶近似式,并以增量的形式表示相应的变量。线性化的公式如下。设非线性函数
其稳定工作点为x0,y0,则线性化后的线性方程为
其中
若非线性函数 其稳定工作点为x10,x20和y0,则线性化后的线性方程为
其中
线性化举例,在液压伺服系统分析中,阀口的流量方程为
式中 Q——通过阀的流量; C——流量系数; x——阀芯位移量或阀的开口度; pL——负载压力; ps——恒定的供油压力 若阀处于某平衡状态时相应的变量为Q0,x0和pL0,则在平衡点附近线性化后,可得线性方程为
式中 ΔQ=Q-Q0; Δx=x-x0; ΔpL=pL-pL0; Kq——流量增益, c——流量压力系数, |