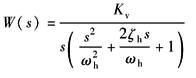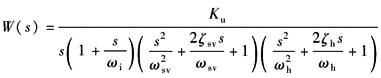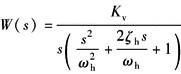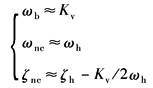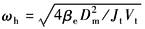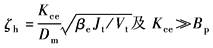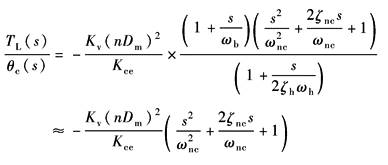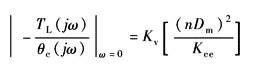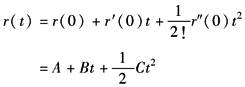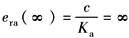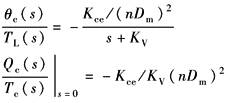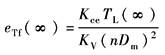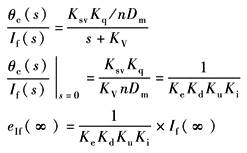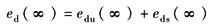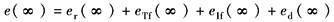电液位置伺服系统的设计计算
电液位置伺服系统的类型及特点
|
电液位置伺服系统的类型及特点 |
||
|---|---|---|
|
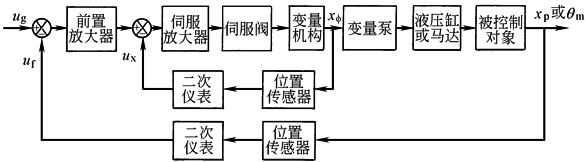
电液位置伺服系统是最常见的液压控制系统,而且在速度、力、功率和热工参量等各种物理控制系统中,也常存在位置内环,因此电液位置伺服系统的分析与设计是分析和设计各类液压控制系统的基础 |
||
|
类型 |
职能表 |
特点 |
|
阀控 电液 位置 控制 系统 |
|
(1)伺服阀的分辨率高、频响高,因而系统的控制精度高、动态响应高 (2)系统效率较低 (3)系统刚度较小 (4)系统阻尼变化大,零位时阻尼最小 (5)控制功率可以高达上百千瓦 (6)应用于要求高精度高响应场合 |
|
泵控 电液 控制 系统 |
|
(1)伺服变量泵的分辨率较低、频响较低,因而系统的控制精度和动态响应较低 (2)系统效率高,特别适于大功率控制 (3)系统刚度较高 (4)系统阻尼低且恒定 (5)用于大功率但精度和响应要求较低的场合 |
电液位置伺服系统的方块图、传递函数及波德图
|
电液位置伺服系统的方块图、传递函数及波德图 |
||
|---|---|---|
|
项目 |
内容分析 |
说明 |
|
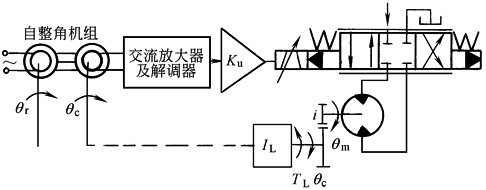
物 理 模 型 |
|
被控制量:负载输出轴角位移θc 控制元件:伺服阀 动力元件:阀控马达 减速装置:一级齿轮减速器 位移检测装置:自整角机组 |
|
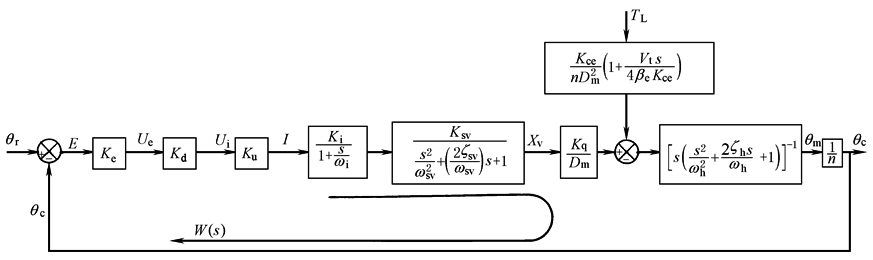
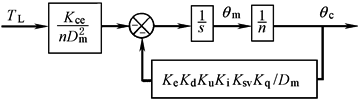
方 块 图 |
|
|
|
开 环 传 递 函 数 |
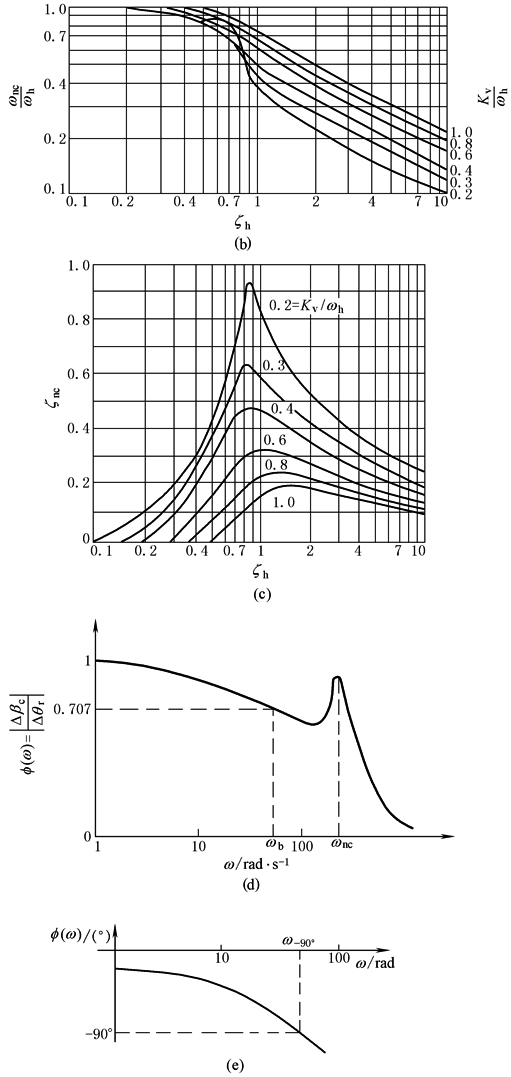
式中 Kv=KeKdKuKiKsvKq/(Dmn) Kv——开环增益,rad/s |
θr、θc——指令输入轴、负载输出轴的角位移,rad E——接收自整角机组转子绕组的感应电势,V Ke——自整角机组的增益,V/rad Ue——解调器的输出电压,V Kd——交流放大器和解调器增益,V/V Ui、Ku——伺服放大器的输出电压(V)、增益(V/V) I——伺服阀线圈电流,A Ki、ωi——线圈回路增益(A/V)、转折频率(rad/s) XV——伺服阀位移,m Ksv——以阀芯位移为输出的伺服阀增益,m/A ωsv、ζsv——伺服阀的频宽,rad/s,阻尼系数(无量纲) θm——液压马达角位移,rad ωh、ζh——液压谐振频率(rad/s)及阻尼系数 i=θm/θc=n i——减速齿轮传动比 T——外负载力矩,N·m L(ω)——对数幅频特性 φ(ω)——对数相频特性 Kv——开环增益,rad/s ωc——穿越(或交轴)频率,rad/s ωL——临界频率,rad/s γ(ωc)——相角稳定裕量,(°) L(ωL)——幅值稳定裕量,dB |
|
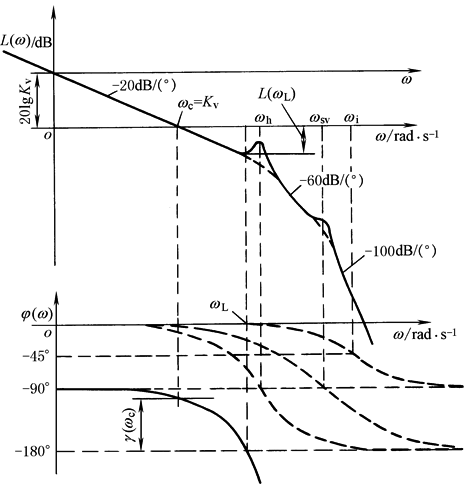
波 德 图 |
|
|
电液位置伺服系统的稳定性计算
|
电液位置伺服系统的稳定性计算 |
||
|---|---|---|
|
类别 方法 |
条件 |
稳定性分析 |
|
简易 稳定 性判 据 |
当ωi?ωsv?ωh,开环传递函数可简化成
|
应用劳斯稳定判据,可得电液位置伺服闭环系统的简易判据:Kv≤2ζhωh 考虑到ζhmin=0.1~0.2 得:Kv≈0.2~0.4ωh |
|
相 对 稳 定 性 判 据 |
当ωi、ωsv、ωh值差别不是很大时,开环传递函数不能简化,即:
注意到液压位置伺服系统具有积分特性,因而仍存在ωc=Kv的情况 |
(1)已知ωi、ωsv、ωh及其阻尼值,并已确定开环增益Kv时,可由波德图中的相角稳定裕量γ(ωc)来评价系统的相对稳定性 一般要求γ(ωc)=30°~60°,具体值视系统要求而定 (2)已知ωi、ωsv、ωh及其阻尼值及要求的γ(ωc),则可由下式计算出允许的开环增益γ(ωc)=180°+φ(ωc)
|
|
动态 仿真 方法 |
当ωi、ωsv、ωh值差别不大,且ωh、ζh、Kv可能在较大范围内变化时 |
可应用面向动态方程、面向方块图、面向传递函数的仿真程序,进行系统的动态数字仿真,分析系统的稳定性、闭环响应及精度,并进行优化设计 |
电液位置伺服系统的闭环频率响应
|
电液位置伺服系统的闭环频率响应 |
||||
|---|---|---|---|---|
|
(1)对指令输入的频率响应计算 |
||||
|
表1 |
||||
|
分类 |
分析方法 |
说明 |
||
|
三 阶 闭 环 系 统 的 简 化 分 析 方 法 |
当开环传递函数可简化成
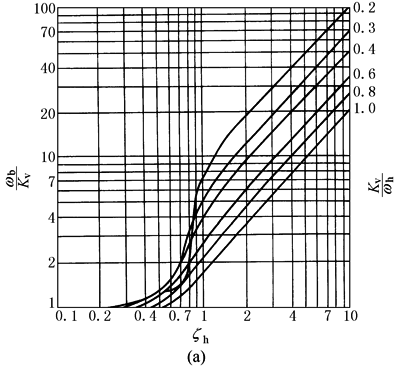
系统结构参数ωh、ζh、Kv已知时,确定ωb、ωnc、ζnc的方法有以下三种 (1)应用劈因法求ωb、ωnc、ζnc。这是一种代数法,计数较麻烦,但可应用有关程序 (2)应用查图表法,即利用ωb/Kv=f(Kv/ωh,ζh)、ωnc/ωh=f(Kv/ωh,ζh)及ζnc=f(Kv/ωh,ζh)三个图表来确定ωb、ωnc、ζnc。这是一种工程简便方法 这三个图表,实际上也是由一系列不同的Kv/ωh、ζh值应用劈因法求出对应的ωb、ωnc、ζnc而绘成的无量纲曲线图 (3)近似估算法,即当ζh、Kv/ωh较小时,认为闭环参数ωb、ωnc、ζnc与开环参数Kv、ωh、ζh有如下近似关系:
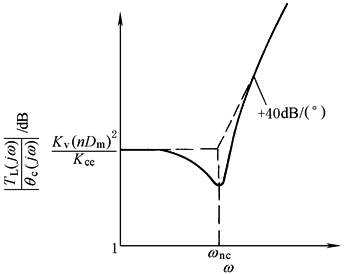
实际上,通常ζhmin=0.1~0.2,Kv/ωh=0.2~0.4,它们确实较小;由三个图表可以看出,此时ωb/Kv略大于1,ωnc/ωh略小于1,上述近似关系成立,三阶闭环系统的闭环频率响应见图d,图中已把ωb近似看做是闭环系统的频宽 由于ωc=Kv,而ωb略大于Kv,因此ωb略大于ωc;ωb与ωc的比值随ζh的增大而增大,因此也可采用如下经验公式: 闭环频宽ω0.707即ω-3db≈(1.2~1.5)ωc 以上简化分析方法用于初步设计是很有用的 |
ωb——一阶因子的转折频率,rad/s ωnc——二阶因子的谐振频率,rad/s ζnc——二阶因子的阻尼系数
|
||
|
高 阶 闭 环 系 统 的 分 析 方 法 |
当开环传递函数W(s)较复杂(4阶或5阶以上)时,计算闭环频率特性f (jω)是极其麻烦的。这时可借助于等M圆图和等N圆图,由开环频率特性分别得图d的闭环幅频特性︱f (ω)︱和图e的闭环相频特性f (ω)。由图d、图e可得闭环频率特性指标: ω0.707——幅值比频宽 ω-90°——相角频宽 ωp——峰值频宽 Mp——峰值 |
|||
|
(2)对负载扰动输入的频率响应计算 |
||||
|
表2 |
||||
|
项目 |
分析 |
说明 |
||
|
闭 环 传 递 函 数 |
|
(1)参见表 电液位置伺服系统的方块图、传递函数及波德图中方块图 (2)设ωi?ωsv?ωh,忽略ωi、ωsv的动态影响 (3)由
有ω1=4βeKce/Vt=2ζhωh (4)因ωb略大于Kv(见表1) Kv略小于2ζhωh,即2ζhωh略大于Kv(见表 电液位置伺服系统的稳定性计算)故ωb≈ω1=2ζhωh |
||
|
闭 环 动 态 位 置 刚 度 |
|
|||
|
闭环 静态 位置 刚度 |
|
(nDm)2/Kce为开环静态位置刚度 说明闭环静态位置刚度比开环增加了Kv倍 |
||
电液位置伺服系统的分析及计算
|
电液位置伺服系统的分析及计算 |
|||||
|---|---|---|---|---|---|
|
误差 类型 |
分析及计算 |
说明 |
|||
|
指令 输入 引起 的稳 态误 差 |
输入信号 r(t) |
阶跃输入 r(t)=A·1(t) |
等速输入 r(t)=Bt |
等加速输入 r(t)=(1/2)ct2 |
(1)液压位置伺服系统属1型系统,r=1 (2)对任意输入信号r(t)在t=0附近展成台劳级数,取前三项有
即任意输入信号可看成是阶跃、等速和等加速输入的合成。与此相应,总的稳态误差为稳态位置误差、速度误差和加速度误差之和 |
|
误差系数 |
稳态位置 误差系数 Kp=∞ |
稳态速度 误差系数 KV=Kv |
稳态加速度 误差系数 Ka=0 |
||
|
稳态误差 er(∞) |
稳态位置误差 erp(∞)= A/(1+Kp) |
稳态速度误差 erv(∞)= B/KV |
稳态加速度误差
|
||
|
负载 扰动 输入 引起 的稳 态误 差 |
由静态方块图可得
负号表示负载增大时位移减小
|
以负载扰动为输入的静态方块图 |
|||
|
零漂 死区 引起 的稳 态 误差 |
|
通常将放大器及伺服阀零漂、伺服阀死区、执行机构的静摩擦力等因素的影响,折算到伺服阀的输入端,以零漂电流If来表示,其静态方块图为
|
|||
|
检测 环节 引起 的稳 态 误差 |
检测装置及传感器的误差将直接传给系统 |
edu(∞)——检测装置的稳态误差 eds(∞)——传感器的稳态误差 |
|||
|
总的 稳态 误差 |
|
|
|||