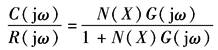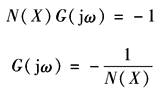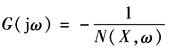非线性反馈控制系统

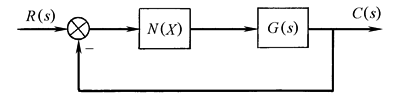
用描述函数法分析非线性控制系统的任务主要是判别系统是否稳定，是否产生自激振荡，确定自激振荡的振幅和频率以及对系统进行校正等。在对非线性系统进行分析时，通常将非线性系统等效变换成以描述函数表示的非线性部分N(X)和以传递函数表示的线性部分相耦合的标准结构形式，如图1所示

图1

稳定性分析

稳定性问题是非线性系统分析中的最主要问题。其分析方法是将线性理论中的奈魁斯特稳定判据推广应用到非线性系统。对于图1所示的非线性系统，其闭环频率特性为

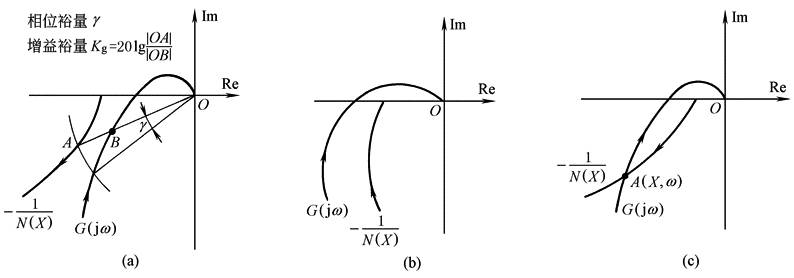
比照线性理论中奈魁斯特稳定判据，当系统处于临界稳定时应满足以下关系，即

或　　　　　　　　　　　　　　　　　　　　　

上式表示，在非线性系统的稳定分析中，-1/N(X)相当于线性系统中复平面上的(-1，j0)点。因此，对非线性系统而言，其稳定的临界点不是固定的，而是一条随输入正弦信号的幅值和频率而变化的轨迹。其稳定性的判别原则是：

① 若线性部分G(s)没有位于S平面右半部的极点，则当G(jω)不包围-1/N(X)时，系统是稳定的，如图2a；

② 若-1/N(X)被G(jω)所包围，则系统不稳定，如图2b；

③ 若G(jω)和-1/N(X)相交，则系统可能产生稳定的等幅振荡，振荡的幅值和频率可根据交点处输入信号幅值和G(jω)的频率来确定，如图2c

对于稳定的非线性系统，同样可以采用增益裕量和相位裕量来衡量其相对稳定性。稳定裕量的计算方法如图2a所示。需要注意的是，对于不同的输入幅值X，-1/N(X)和G(jω)的相对位置是不同的，因此稳定裕量是一个变化的数，通常以其最小值来衡量非线性系统的相对稳定性

非线性系统的稳定性分析也可以在尼柯尔斯图上进行

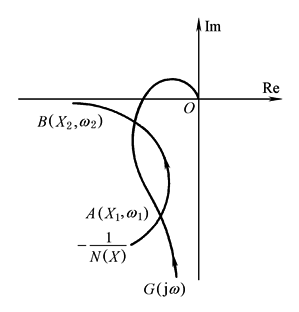
图2

振荡稳定性分析

设非线性系统具有图3所示的特性，-1/N(X)和G(jω)有两个交点，A(X₁，ω₁)和B(X₂，ω₂)，图中箭头表示输入幅值X和频率的增加方向。振荡是否稳定的判别原则是：

① 如果沿-1/N(X)曲线按X增大方向变动时，-1/N(X)由G(jω)的外部走向G(jω)的包围圈内，则此交点不是稳定的振荡点，是具有发散特性的不稳定工作点，如图中的A点；

② 如果沿-1/N(X)曲线按X增大方向变动时，-1/N(X)由G(jω)的内部走向G(jω)的外部，则此交点是稳定的振荡点，称为自激振荡或极限环，振荡幅值和频率分别为X₂和ω₂，如图中的B点

对于如图3特性的非线性系统，当输入幅值X较小时，系统将是稳定的；而输入幅值X较大时，系统可能趋向一个平衡状态，也可能趋向一个稳定的振荡。因此描述函数与输入幅值和频率有关，即N(X，ω)。稳定性的判别条件为

此时-1/N(X，ω)将是随ω变化的曲线簇

图3

消除自激振荡的方法

非线性因素的存在，往往给系统带来不利的影响，如误差增大、响应迟钝以及产生自振等等。其中低频自振尤为不利，常需要采取一定的措施以消除自激振荡。常用的方法有：

① 减小系统的开环增益；

② 利用串联超前校正和位置或速度反馈校正，改善线性部分的特性；

③ 引入新的非线性以改变原非线性的特性

非线性特性的利用

在某些情况下，如果在线性系统中恰当引入非线性环节，能起到改善线性系统性能的作用，这种方法已广泛应用于工程实际。例如：

图4　　　　　　　　　　　　　　　　　　　　　　　　　　　图5

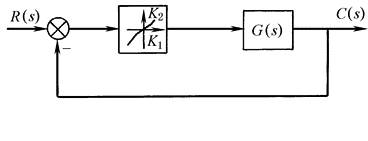
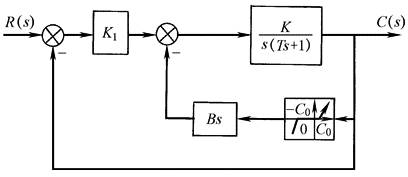
① 在伺服控制系统中引入可变增益放大器，如图4所示；

② 实现非线性阻尼控制，如图5所示；

③ 非线性积分器，如图6所示，这类积分器的相位迟后比线性积分器的要小，因此有利于改善系统的动态性能；

④ 利用振荡线性化以消除死区、摩擦和继电器非线性的影响

振荡线性化是在非线性元件的输入端，外加一个高频小振幅的振荡信号，使相应的部件处于颤振状态。因此在没有控制信号输入时，非线性元件呈等幅振荡，输出的平均值为零；有控制信号输入时，由于输出偏振，所以对非线性元件之后的线性元件，相当于使非线性元件在零位附近线性化了。采用振荡线性化时，颤振信号可以来自系统内部也可由外部输入

图6

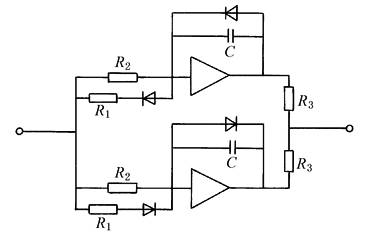
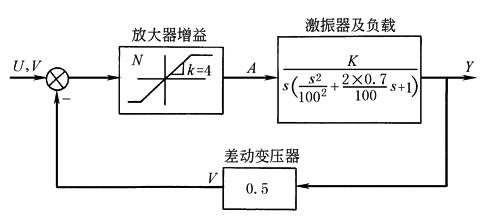
非线性系统分析举例

图7所示为一电控振动台，其放大器呈饱和特性，不饱和段的斜率k＝4A/V。激振器和负载的增益K＝63.2cm/A

根据系统的开环传递函数和饱和非线性的描述函数可给出系统的奈魁斯特图G_k(jω)和非线性元件的特性-1/N(X)曲线，如图8所示

图7

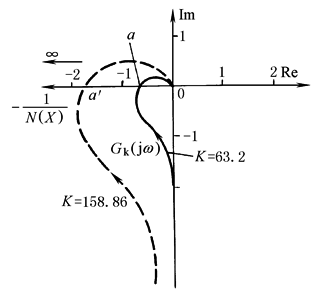
图8

显然，G_k(jω)和-1/N(X)有交点a，且为自激振荡点，其幅值为1×10^-9cm，振荡频率为16Hz。这一振荡属于低频极小振幅的自激振荡。若系统的线性部分的增益增大到158.86cm/A，则G_k(jω)变为图中的虚线且与-1/N(X)相交于a' 点，相应振荡幅值和频率为0.01cm和17.5Hz的自激振荡。这一振荡不能被忽视