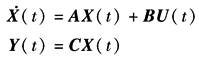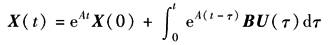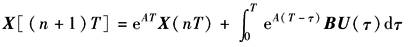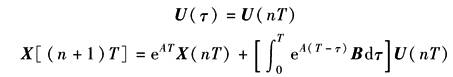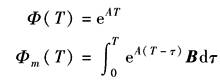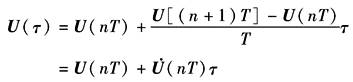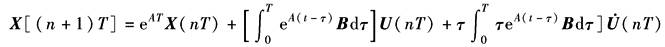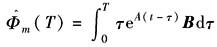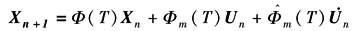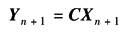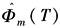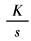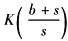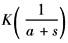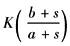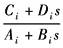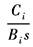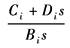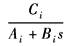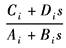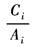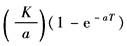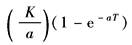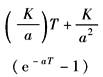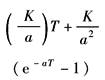控制系统的仿真

离散相似法数字仿真是以系统的函数方框图为数学模型，并以模型中所包含的典型环节将系统的数学模型离散化。在仿真过程中各环节独立地计算其输出，由连接矩阵建立各环节之间的关系，这种方法的仿真速度较快，且能插入非线性环节，所以能比较方便地推广应用于非线性系统的仿真

离散相似法是在系统的各环节前加入虚拟的采样-保持器得到其离散化的模型，如图1所示

图中X(t)是环节的状态变量。环节的状态方程和输出方程分别为

状态方程的时域解为

对上式进行离散化，并设环节前虚拟的采样——保持器的采样周期为T，则对于t＝nT和t＝(n+1)T的两任意相邻时刻状态变量的关系为

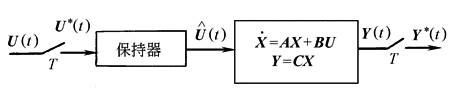
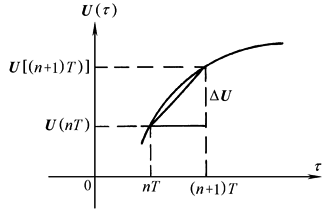
虚拟保持器的存在，使输入函数U(τ)将具有不同形式，如图2所示

图1

图2

(1)若为零阶保持器

因此　　　　　　　

令　　　　　　　　　　　　　　　　　

代入上式并写成递推式

(2)若为一阶保持器

因此

令　　　　　　　　　　　　　　　　　　　

代入上式并写成递推式，则

根据各环节的输出方程，可得

显而易见，离散方程系数Φ(T)，Φ_m(T)和决定于环节的状态方程系数矩阵A和B，编制适当程序即可依次递推计算出X_n+1和Y_n+1

在实际应用中，通常将控制系统中的典型环节分类，并分别求出相应的离散系数表达式和输出方程表达式，如下表所示

典型环节离散方程系数和输出方程

系数

积分环节

比例+积分

惯性环节

超前-滞后

比例

环节类型H

0

1

2

3

4

典型传

递函数

K

K

C_i/B_i

C_i/B_i

C_i/B_i

D_i/B_i

C_i/A_i

a

0

0

A_i/B_i

A_i/B_i

0

b

0

D_i/C_i

0

C_i/D_i

0

Φ(T)

1

1

e^-aT

e^-aT

0

Φ_m(T)

KT

KT

K

KT²/2

KT²/2

0

输出方程

Y_n+1＝X_n+1

Y_n+1＝X_n+1+KbU_n+1

Y_n+1＝X_n+1

Y_n+1＝(b-a)X_n+1+KU_n+1

Y_n+1＝X_n+1

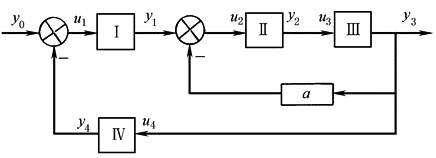
(1)连接矩阵

对于图1所示系统，各环节间的关系可以用连接矩阵来描述，从而构成闭环系统

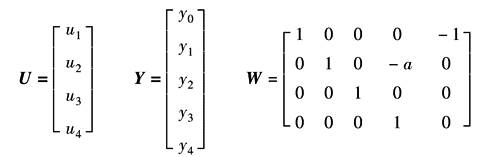
图中　u₁＝y₀-y₄

u₂＝y₁-ay₃

u₃＝y₂

u₄＝y₃

其矩阵表示式为

U＝WY

图1

其中

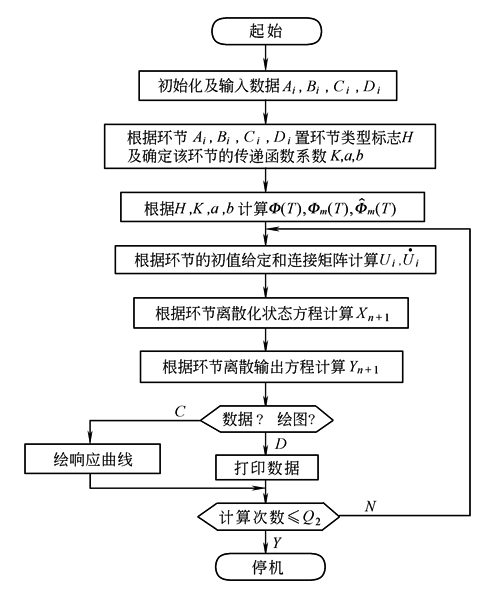
W称为连接矩阵，它反映了系统中各环节之间的关系，如W_ij表示第i号环节受第j号环节输出y_j作用的作用系数

(2)仿真程序框图及说明

利用离散相似法进行连续系统数字仿真的程序框图如图2所示

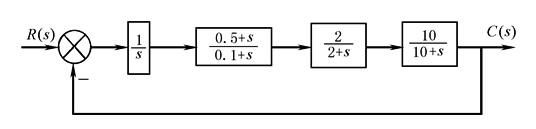
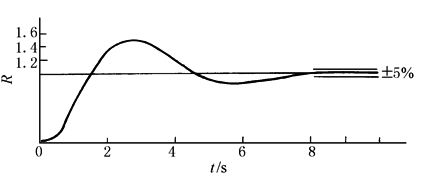
图2

例如，一控制系统如图3所示，利用系统数字仿真程序，可得仿真的控制系统的响应曲线如图4所示，并打印出，上升时间t_r＝1.6s，最大超调量σ_p＝52%，调整时间t_s＝6.8s

图3

图4  控制系统阶跃响应曲线