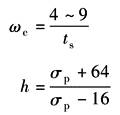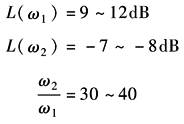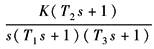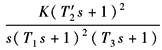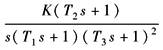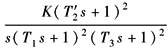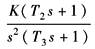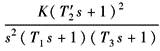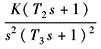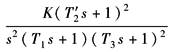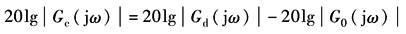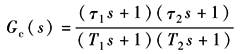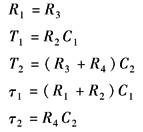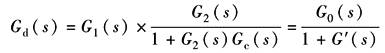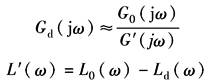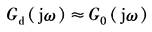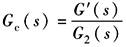线性控制系统的校正

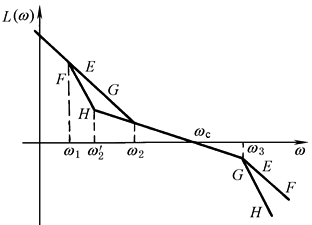
利用期望对数频率特性来确定校正装置的结构形式，是工程上常用的设计方法之一

根据对控制系统的精确度和动态品质的要求所绘出的与性能指标相对应的对数频率特性，称为系统的期望特性。将期望特性和原系统的特性进行比较后，根据它们的差可以确定校正装置的传递函数，最后查表 常用的校正装置中表1确定校正装置的结构形式

控制系统的对数频率特性主要分为三个区：低频区由系统的开环增益和系统的无差度决定，它规定了系统的稳态品质；中频区规定了系统的稳定性和动态品质，中频区主要由增益交界频率ω_c、截止频率ω_b、相位裕量γ和中频宽度h等要素决定；高频区对系统的品质影响较小，但与系统抑制噪声的能力有关。期望对数频率的绘制大致步骤如下

① 根据系统的无差度υ和开环增益K，绘制斜率-20dB/dec的低频渐近线，渐近线在ω＝1处的增益L≥20lgK。在低频区主要采用高增益原则绘制期望特性

② 根据对系统的动态品质如超调量σ_p和调整时间t_s的要求求取期望特性的增益交界频率ω_c，在ω_c处绘斜率为-20dB/dec的中频渐近线，渐近线向两个方向延伸一定的中频宽度h，初步设计时，ω_c和h可以用以下公式估算：

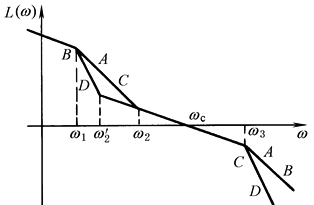
中频段宽度h直接影响到系统的稳定性和动态品质。经验证明中频段的边界位置可参考以下取值范围：

式中　ω₁——中频段的低频端频率值；

ω₂——中频段的高频端频率值

③ 高频区的渐近线可以与原系统的高频特性相重合，以有利于简化校正装置结构

④ 低频与中频过渡区，中频与高频过渡区的连接应注意尽量使相连各段的渐近线斜率彼此相差不超过-40dB/dec

利用上述步骤绘制的期望特性是否能满足所要求的系统性能指标需要进行校核，校核可以采用计算机数字仿真的方法来进行。下表是几种典型工程中常用的期望特性模型

典型工程中常用的期望特性模型

特性类型

对数幅频特性曲线

各频段的斜率/dB·dec^-1

(低频→高频)

对应的开环传递函数

Ⅰ型系统

(一阶无差系统)

A

-20

-40

-20

-40

B

-20

-60

-20

-40

C

-20

-40

-20

-60

D

-20

-60

-20

-60

Ⅱ型系统

(二阶无差系统)

E

-40

-40

-20

-40

F

-40

-60

-20

-40

G

-40

-40

-20

-60

H

-40

-60

-20

-60

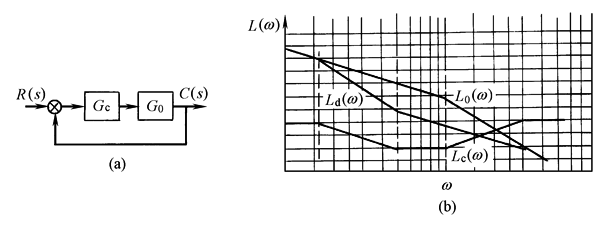
(1)串联校正装置的确定

串联校正如图1a所示，其中G₀(s)为系统原有部分的传递函数，G_c(s)为串联校正装置的传递函数，期望特性的传递函数为G_d(s)，校正后系统应满足：G_d(s)＝G_c(s)G₀(s)

相应的对数频率特性为

根据上式确定的校正装置对数频率特性如图1b所示

图1

校正装置的传递函数为

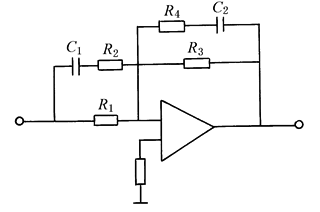
由表常用的校正装置中表2可得到校正装置的结构和相应的元件参数，如图2所示

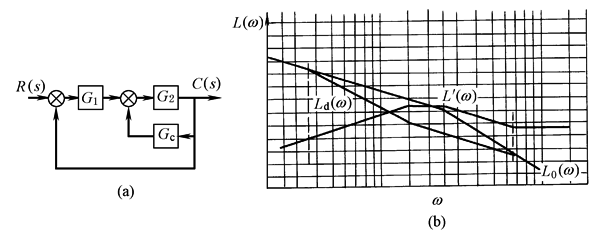
图2

(2)反馈校正装置的确定

反馈校正如图3a所示，其中G₁(s)，G₂(s)为系统的原有部分传递函数，G_c(s)为反馈校正装置传递函数，期望特性为G_d(s)，校正后系统应满足

当︱G₂(jω)G_c(jω)︱?1时

因此　　　　　　　　　　　　　　　　　

当︱G₂(jω)G_c(jω)︱=1时

因此，期望特性L_d(ω)和原系统的L₀(ω)相重合

确定校正装置时，先分别绘出L₀(ω)和L_d(ω)，然后以L_d(ω)和L₀(ω)的重合点为分界，分出︱G₂(jω)G_c(jω)︱?1的频率范围，并利用上述两个关系求出L'(ω)，如图3b所示

图3

根据L'(ω)可求出反馈校正装置的传递函数G_c(s)：

通常还要根据G'(s)校核校正回路的稳定性。在回路稳定的条件下，即可以根据G_c(s)查表确定校正装置的结构及其相应参数