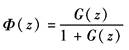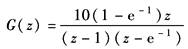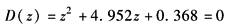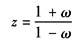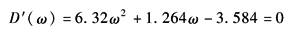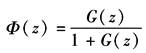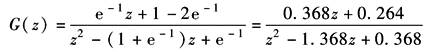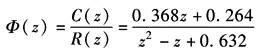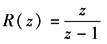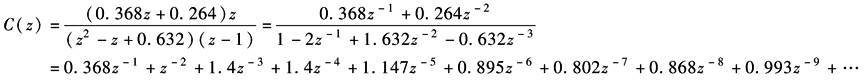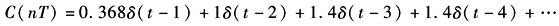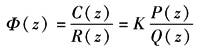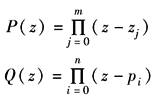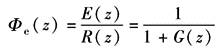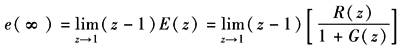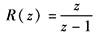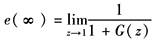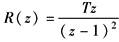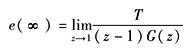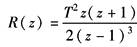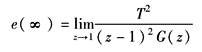线性离散控制系统

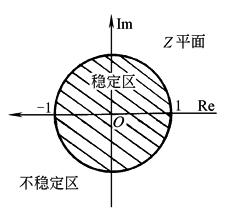
(1)稳定条件

离散控制系统稳定的充要条件是其特征方程的根全部分布在Z平面上以原点为圆心的单位圆内。如图1所示

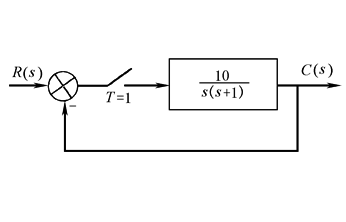
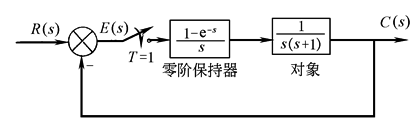
图1　　　　　　　　　　　　　　　　　　　　　　　　图2

(2)劳斯稳定判据

其判别步骤如下：

① 求出离散系统的特征方程D(z)＝0；

② 在D(z)＝0中令z＝(1+ω)/(1-ω)，求出新方程D'(ω)＝0；

③ 利用劳斯表判别D'(ω)＝0的根是否均为负实部。若D'(ω)的根全部具有负实部，则D(z)＝0的根全部位于Z平面的单位圆内

例　离散系统如图2所示

系统的闭环脉冲传递函数为

其中　　　　　　　　　　　　　　　　

因此　　　　　　　　　　　　　　

令　　　　　　　　　　　　　　　　　　　　

则　　　　　　　　　　　　　　

列劳斯表

劳斯表第一列元素符号变化一次，因此D'(ω)有一个根具有正实部，故D(z)中有一个根位于Z平面上的单位圆之外，系统不稳定

评价离散系统过渡过程品质时，仍以单位阶跃信号作为输入信号，以超调量、过渡过程时间等特征量来描述系统的性能

(1)单位阶跃响应

设系统如图1所示

图1

系统的闭环脉冲传递函数为

其中　　　　　　　　　　　　　　　　　

故　　　　　　　　　　　　　　　　　　　　　　

单位阶跃输入时

则

Z反变换后

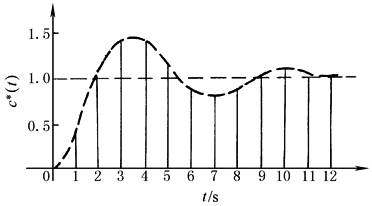
输出信号C*(t)如图2所示

该系统的单位阶跃响应是衰减振荡，相应的特征值为

c*(∞)＝1

σ_p＝40%

t_s＝10s(Δ＝0.05)

(2)离散系统的极点分布和瞬态响应之间的关系

离散系统的闭环脉冲传递函数为

其中

图2

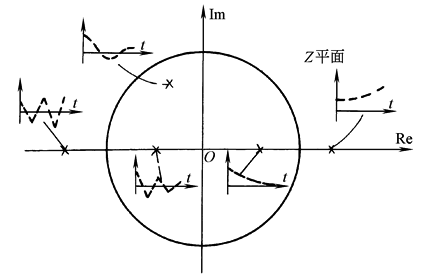
式中　K——常数；

z_j——系统的零点；

p_i——系统的极点

则p_j在Z平面上的位置与系统瞬态响应的关系如图3所示

图3  极点位置与瞬态响应的关系

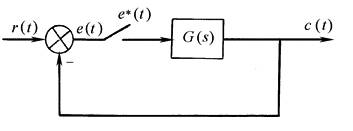
对于如下图所示的离散系统，其误差脉冲传递函数F_e(z)为

利用终值定理，可计算系统的稳态误差e(∞)

对于典型的输入函数，系统的稳态误差计算见下表

典型输入作用下稳态误差计算式

输入信号R(z)

e(∞)计算式

单位阶跃信号

单位斜坡信号

单位加速度信号