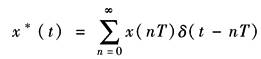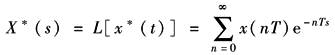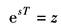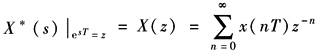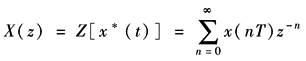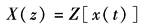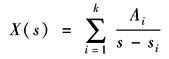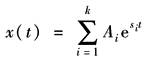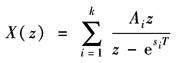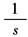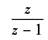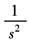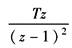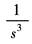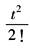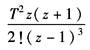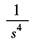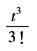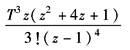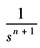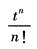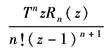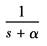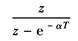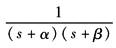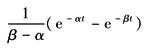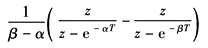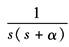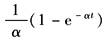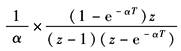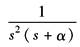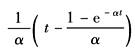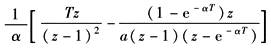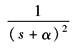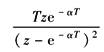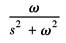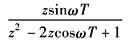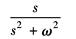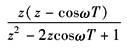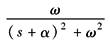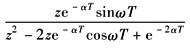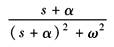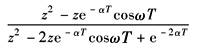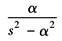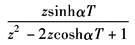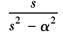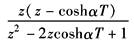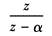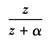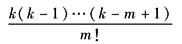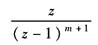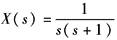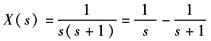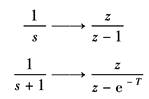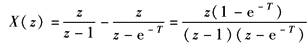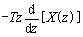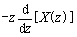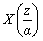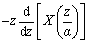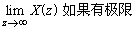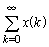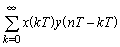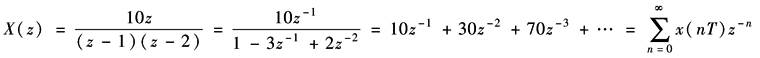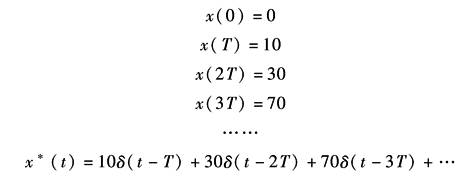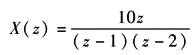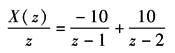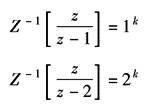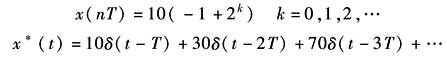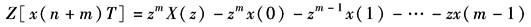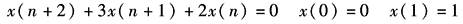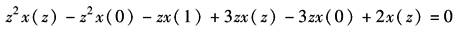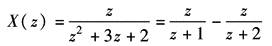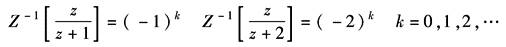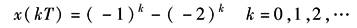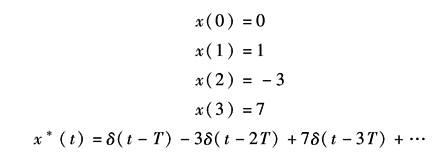线性离散控制系统

Z变换是研究离散系统的一种有力工具，利用它可将线性差分方程变换成线性代数方程

设离散信号x*(t)为

则其拉氏变换式为

令　　　　　　　　　　　　　　　　　　　　　　　

则　　　　　　　　　　　　

式中，X(z)称为x*(t)的Z变换，并以Z[x*(t)]表示，即

X(z)有时也习惯性地称作x(t)的Z变换式，即

而其实际含义仍是指x(t)经采样后，对x*(t)的Z变换

Z变换式的求取方法有两种，即根据连续信号x(t)求X(z)或根据x(t)的象函数X(s)求取相应的Z变换式，后者称为部分分式法。部分分式的原理是：设X(s)具有以下形式

式中　k——X(s)中的极点数；

A_i——对应于每一个极点的常数；

s_i——X(s)的极点

则X(s)的原函数x(t)为

利用基本函数的Z变换表，可得与x(t)相对应Z变换式

基本函数的Z变换如下表所示

Z变换表

X(s)

x(t)或x(k)

X(z)

1

δ(t)

1

e^-kTs

δ(t-kT)

z^-k

1(t)

t

e^-αt

te^-αt

sinωt

cosωt

e^-αtsinωt

e^-αtcosωt

sinhαt

coshαt

α_k

α^kcoskπ

例　已知

因为　　　　　　　　　　　　　　　

查上表，可得

因此　　　　　　　　　　　　

x(t)或x(k)

Z[x(t)]或Z[x(k)]

αx(t)

αX(z)

x_i(t)+x₂(t)

X₁(z)+X₂(z)

x(t+T)或x(k+1)

zX(z)-zx(0)

x(t+2T)

z²X(z)-z²x(0)-zx(T)

x(k+2)

z²X(z)-z²x(0)-zx(1)

x(t+kT)

x^kX(z)-z^kx(0)-z^k-1x(T)-…-zx(kT-T)

x(k+m)

z^mX(z)-z^mx(0)-z^m-1x(1)…-zx(m-1)

tx(t)

kx(k)

e^-αtx(t)

X(ze^αT)

e^-αkx(k)

X(ze^α)

α^kx(k)

kα^kx(k)

x(0)

x(∞)

X(1)

X(z)Y(z)

Z反变换是根据X(z)求出原函数x*(t)和x(nT)。常用Z反变换的方法有以下两种

① 幂级数法。幂级数法是利用长除把X(z)展开成z^-i的幂级数式，然后根据Z变换的定义式求出x*(t)或x(nT)。例如

因此

这种方法有时不便于求取x(nT)的闭式结果

② 部分分式法。这是一种常用方法，它将X(z)分解成为部分分式，然后利用Z变换表求取x*(t)或x(nT)，例如

展开成部分分式

查表Z变换定义中表可得

因此　　　　　　　　　　　　

用Z变换求解差分方程与用拉普拉斯变换解微分方程一样，是非常有用的，其实质是利用Z变换将差分方程转化为代数方程。由Z变换的性质知，x[(n+m)T]的Z变换式为

式中，x(0)，x(1)，…是x(t)在不同时刻的采样值。利用上述关系就可以将差分方程转化为以z为变量的代数方程，并自动包含了初始采样值。例如差分方程

方程两端Z变换后得

代之初始数据并整理之

利用Z变换表可得

因此X(z)的原函数x(kT)为

各时刻的函数值为