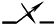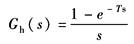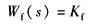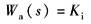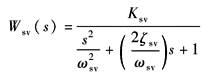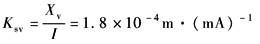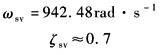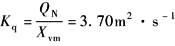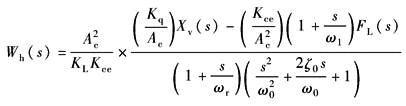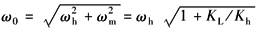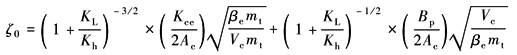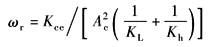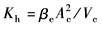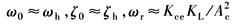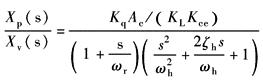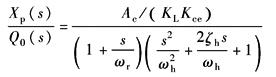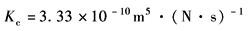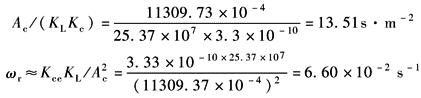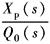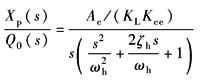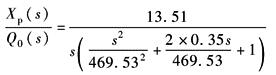液压伺服系统设计实例

项目

内容

方

块

图

由于APC系统采用工业控制数字计算机或数字控制器，因此它是一个离散控制系统，方块图如下：

图中　 X_p——压下缸活塞位移，被控制量

R——AGC控制器发出的指令。当对APC系统进行测试时，R为阶跃或正弦试验信号，因此须通过采样器将其离散化

——采样器，它把连续的模拟信号转换成周期为T的一串脉冲——离散的模拟信号。离散的模拟信号再经A/D转换(图中未画出)变成

离散的数字信号传递给CPU

Y——由检测环节输出的位置反馈信号。信号的型式取决于传感器类型

D——工业控制计算机或数字控制器。可令D＝K₁，K₁——增益调整系数

D/A——数模转换器，它把离散数字信号转换成离散模拟信号。其转换精度取决于位数大小。由于D/A和A/D只影响转换精度而不会影响系统的基本性能，所以方块图中可以省略

各

环

节

传

递

函

数

零阶保持器

由于零阶保持器简单，相位滞后小，一般都采用零阶保持器，其传递函数G_h(s)把离散的模拟信号近似恢复成连续的模拟信号

位移传感器及其二次仪表

由于压下系统中均需选用高精度、高响应的位置传感器及其配套二次仪表，因此：

W_f(s)——位移传感器及其二次仪表传递函数

对于LVDT或电感式位移传感器及其二次仪表，它是以电压输出的连续模拟信号，须经采样器变成离散模拟信号，再经A/D转换成离散数字信号。对于磁尺及其检测器(二次仪表)，它输出的是脉冲宽度为微米级的脉冲，需经高速计数器计数。对于磁致伸缩式位移传感器，它有模拟式和数字式两种可供选择，数字式中又有SSI和CANBUS两种接口板

K_f——检测环节增益，本例中K_f＝156.25V·m^-1

放大器

考虑到伺服放大器频宽比伺服阀高得多，于是：

W_a(s)——伺服放大器传递函数

K_i——放大器(PID)的比例增益，K_i＝4~100mA·V^-1可调

调定K_i＝15mA·V^-1

伺服阀

W_sv(s)——伺服阀的传递函数

K_sv——伺服阀的增益，以电流I_N为输入、以主阀芯位移X_v为输出时

ω_sv——伺服阀的频宽，rad·s^-1

ζ_sv——伺服阀的阻尼系数

根据伺服阀频宽特性可知

伺服阀的流量增益

以流量为输出时，伺服阀的总增益K'_sv＝K_svK_q＝6.67×10^-4m³·(s·mA)^-1

动力元件

W_h(s)——动力元件，即压下缸及其负载的传递函数

严格地讲，APC系统动力元件属于多自由度动态系统。由于轧件的变形抗力系数，K_L=K(K为轧机自然刚度)，作为工程分析，可将其看做是单自由动态系统。并可直接引用表 阀控动力元件与负载特性的匹配及表 三通阀控制不对称缸的动态特性中的分析结论，直接写出带有弹性负载K_L时的传递函数

式中

ω₀——综合谐振频率，rad·s^-1

ζ₀——阻尼系数

ω_r——综合刚度引起的转折频率，rad·s^-1

K_h——液压弹簧刚度，N·m^-1

K_L——弹性负载刚度，N·m^-1

由于，因此：

则以X_v为输入，以X_p为输出时，传递函数为

而以Q₀为输入，以X_p为输出时的传递函数为

压下缸内泄漏极其微小，于是K_ce＝K_c，阀在工作点处的流量-压力系数K_c可从其静态特性中估计出来

取K_L＝25.37×10⁷N·m^-1，则

因ω_r=ω_h，故可将写成

APC系统动力元件属于多自由度动态系统。由于轧件的变形抗力系数K_L=K(K为轧机自然刚度)，APC系统工作时，伺服阀不可能在零位，总是在零位附近调节，一旦偏离零位，则阻尼便迅速增大，可取ζ_h＝0.3~0.35。于是

最

终

方

块

图

综上可得以AGC指令R为输入，以X_p为输出的APC系统闭环状态方块图：