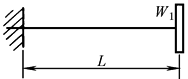
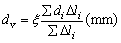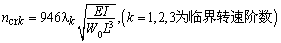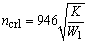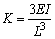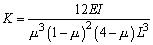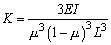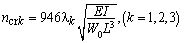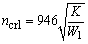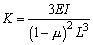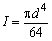不带圆盘的均匀质量轴的临界转速
轴的临界转速校核
|
轴的临界转速校核 |
|---|
|
轴系(轴和轴上零件)是一个弹性体,当其回转时,一方面由于本身的质量(或转动惯量)和弹性产生自然振动, 有其自振频率;另一方面由于轴系各零件的材料组织不均匀、制造误差及安装误差等原因造成轴系重心偏移;导致回转时产生离心力、从而产生以离心力为周期性干扰外力所引起的强迫振动,有其强迫振动频率。当强迫振动的频率与轴的自振频率接近或相同时,就会产生共振现象,严重时会造成轴系甚至整台机器的破坏。产生共振现象时轴的转速称为轴的临界转速。临界转速的校核就是计算出轴的临界转速,以便使工作转速避开临界转速。 轴的振动的主要类型有横向振动(弯曲振动)、扭转振动和纵向振动。一般轴最常见的是横向振动,故本节仅介绍横向振动临界转速的校核。 临界转速在数值上与轴横向振动的固有频率相同。一个轴在理论上有无穷多个临界转速。按其数值由小到大分别称一阶、二阶、三阶……临界转速。为避免轴在运转中产生共振现象,所设计的轴不得与任何临界转速相接近,也不能与一阶临界转速的简单倍数重合。 转速低于一阶临界转速的轴一般称为刚性轴,高于一阶临界转速的轴称为挠性轴,机械中多采用刚性轴;但转速很高的某些轴(如离心机、汽轮机的轴),如采用刚性轴,则所需直径可能过大,使结构过于笨重,故常用挠性轴。 对转速较高、跨度较大而刚性较小,或外伸端较长的轴,一般应进行临界转速的校核计算,使工作转速避开临界转速,并使其在各阶临界转速一定范围之外。对于刚性轴,应使n<0.75ncr1,对于挠性轴,应使n>1.4ncr1且n<0.7ncr2(n为轴的工作转速;ncr1为轴一阶临界转速;ncr2为轴二阶临界转速)。 轴临界转速大小与材料的弹性特性,轴的形状和尺寸,轴的支承形式和轴上零件的质量等有关,与轴的空间位置(垂直、水平或倾斜)无关。 阶梯轴临界转速的精确计算比较复杂,作为近似计算,可将阶梯轴视为当量直径为dv的光轴进行计算,当量直径dv按下式计算: 式中 di——第i段轴的直径,mm; △li——第i段轴的长度,mm; ξ——经验修正系数。若阶梯轴最粗一段或几段的轴段长度超过轴全长的50%时,可取ξ =1;小于15%时,此段当作轴环,另按次粗轴段来考虑。在一般情况下,最好按照同系列机器的计算对象,选取有准确解的轴试算几例,从中找出 ξ 值。例如一般的压缩机、离心机、鼓风机转子可取ξ =1.094。 |
横向振动时轴的临界转速ncr
|
横向振动时轴的临界转速ncr r/min |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
|
均匀质量轴的临界转速
|
带圆盘但不计轴自重时轴的一阶临界转速
|
||||||||
|
|
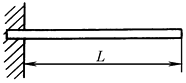
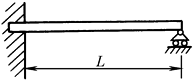
λ1=3.52 λ2=22.43 λ3=61.83 |
|
|
||||||
|
|
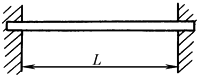
λ1=9.87 λ2=39.48 λ3=88.83 |
|
|
||||||
|
|
λ1=15.42 λ2=49.97 λ3=104.2 |
|
|
||||||
|
|
λ1=22.37 λ2=61.67 λ3=120.9 |
|
|
||||||
|
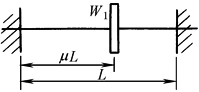
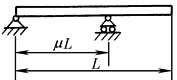
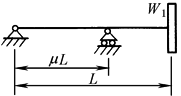
均匀质量轴的临界转速
|
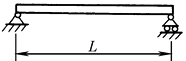
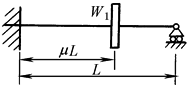
带圆盘但不计轴自重时轴的一阶临界转速
|
||||||||
|
|
|
|
|||||||
|
μ |
0.5 |
0.55 |
0.6 |
0.65 |
0.7 |
0.75 |
|||
|
λ1 |
8.716 |
9.983 |
11.50 |
13.13 |
14.57 |
15.06 |
|||
|
μ |
0.8 |
0.85 |
0.9 |
0.95 |
1.0 |
||||
|
λ1 |
14.44 |
13.34 |
12.11 |
10.92 |
9.87 |
||||
|
|
|||||||||
|
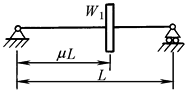
注:1.各种支座情况下,等直径轴在横向振动时的第一、二、三阶临界转速计算公式见本表 2.W0——轴自重,N;W1——圆盘所受的重力,N;L——轴的长度,mm;λk——支座形式系数;E——轴材料的弹性模量,对钢,E=206×103MPa;I——轴截面的惯性矩,mm4, |
|||||||||