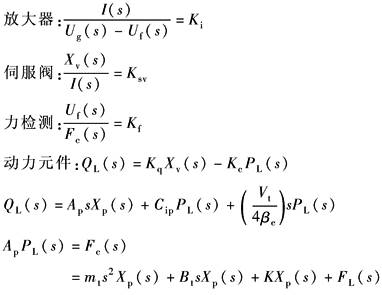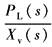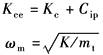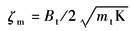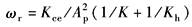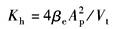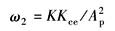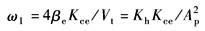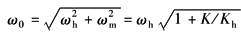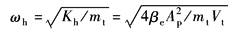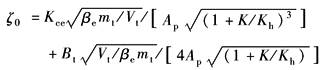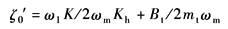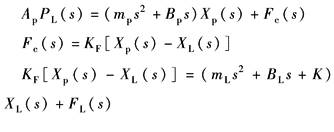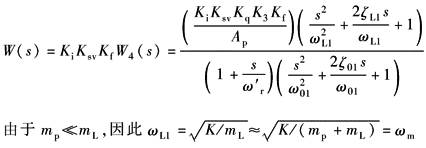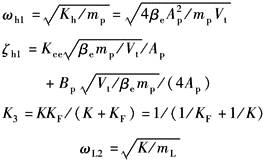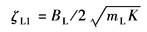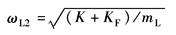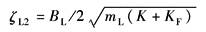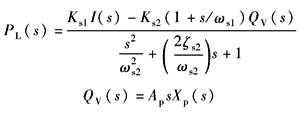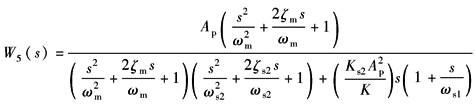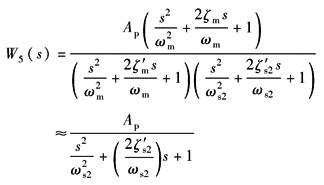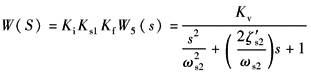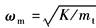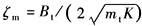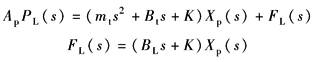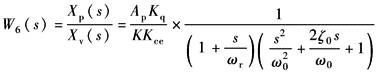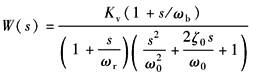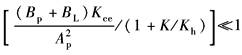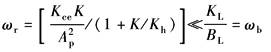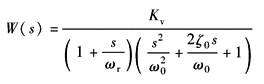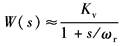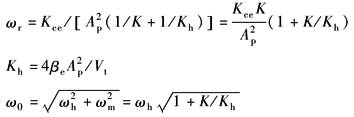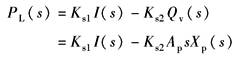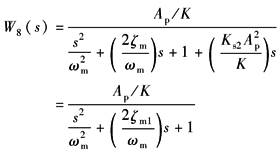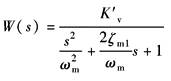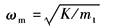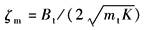电液伺服系统的设计计算

如果说电液速度伺服系统可能受到电气控制系统的挑战，电液力伺服系统却是独树一帜，因为用液压缸对受控对象进行加载极为简便，且出力大、尺寸小、响应快、精度高。电液力(压力)伺服系统广泛应用于材料试验机、大型构件试验机、航空或高速汽车轮胎试验机、负载模拟器、飞机防滑车轮刹车系统、带材张力调节系统、平整机恒压系统和水压试管机压力控制等方面

类型

驱动力伺服系统

负载力伺服系统

系统

组成

特点

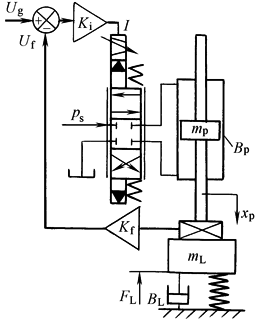
力传感器装在施力缸活塞与被控制对象之间，检测到的力包括惯性力、黏性阻尼力和弹性力；因此检测和控制的是施力缸的驱动力

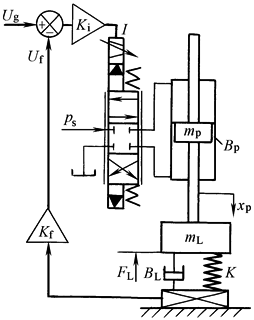
力传感器装在被控制对象与基座之间，检测和控制的仅是弹性负载力

项目

分析

说明

动

态

方

程

力传感器刚度K_f?K(负载刚度)时，可把力传感器看成刚性，系统看做是单自由度系统

F_c——力传感器的输出力，N

U_f——力传感器二次仪表的输出，V

K_f——力传感器及二次仪表的增益，V/N

m_t＝m_p+m_L——总的运动质量，kg

B_t＝B_p+B_L——总的黏性阻尼系数，N·s/m

K——负载刚度，N/m

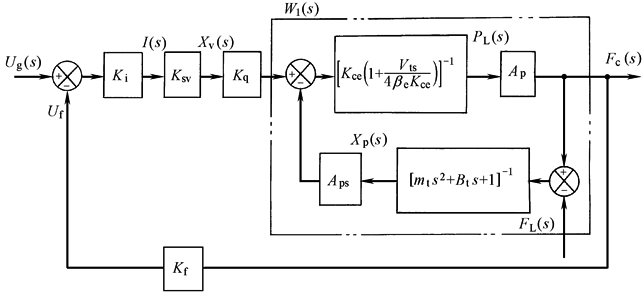
方

块

图

开

环

传

递

函

数

W(s)＝K_iK_svK_fK_qW_l(s)

考虑到：F_c(s)＝A_pP_L(s)

可直接引用表 传递函数及其简化中结果，可得：

K_v＝K_iK_svA_pK_fK_q/K_ce

K_v——开环增益

ω_m——机械谐振频率，rad/s

ζ_m——机械阻尼系数，无量纲

ω_r——液压及机械弹簧引起的转折频率，rad/s

K_h——液压弹簧刚度，N/m

ω₂——负载弹簧引起的转折频率，rad/s

ω₁——液压弹簧引起的转折频率，即容积滞后频率，rad/s

ω₀——综合谐振频率，rad/s

ω_h——液压谐振频率，rad/s

ζ₀——综合阻尼系数，无量纲

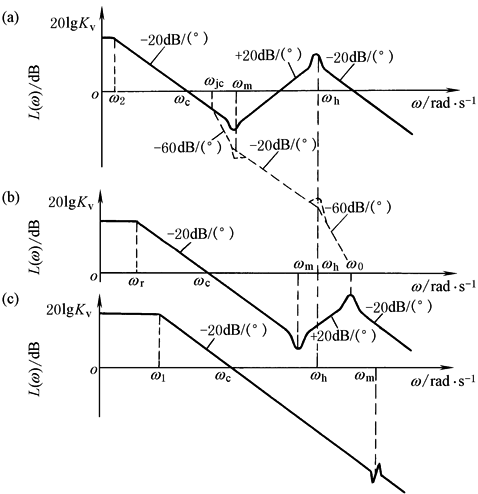
波

德

图

(a)K=K_h的情况

(b)K与K_h相当情况

(c)K?K_h的情况

结论：

(1)驱动力系统属0型系统，对阶跃输入存在稳态误差

(2)负载刚度K愈小，系统稳定性愈差，甚至ω_h处的谐振峰可能超出零分贝线，以致不稳定，如波德图a所示。在ω_c与ω_m之间加入W_c(S)＝(1+s/ω_c)^-2的校正环节，可望改善稳定性，见a图中虚线。当然，仅当K变化不大时，校正才会奏效

(3)在相同的开环增益下，K愈小，ω_c愈低，即响应速度愈低。因此系统稳定性和响应均应按K最小值来检验

(4)对于实际的驱动力系统，不仅要充分考虑K变化对系统性能的影响，还应计及伺服阀等小参数的影响

(5)若要分析外负载力F_L对输出力F_c的影响，还应进行类似的分析

项目

分析

说明

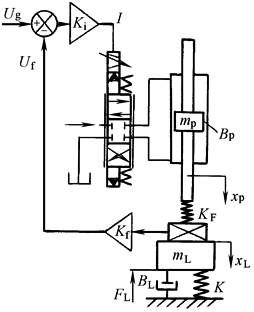
物

理

模

型

及

动

态

方

程

与单自由度系统相比，仅力平衡方程不同：

K_F——力传感器刚度，N/m

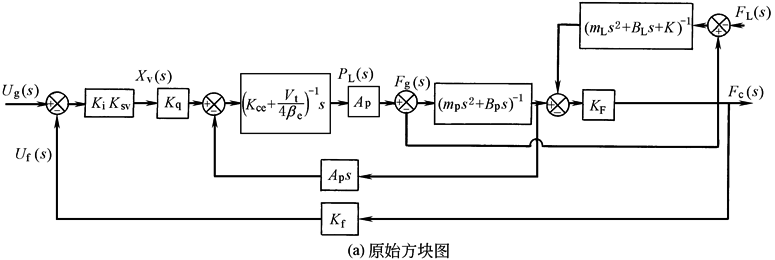
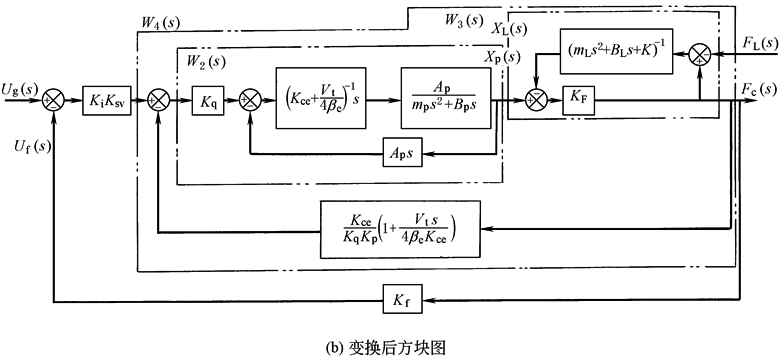
方

块

图

及

其

简

化

开

环

传

递

函

数

及

分

析

图b中W₂(s)相当于不存在弹性负载的阀控缸以X_v为输入，以X_p为输出的传递函数，可直接引用表传递函数及其简化中K＝0的结论：

如ω₀₂?ω₀₁，则ω₀₂所处的二阶环节可略去，此时

ω_L2——负载谐振频率

ζ_L1——负载阻尼比

ω_L2——负载力及传感器的综合谐振频率

ζ_L2——综合阻尼比

ω'_r、ω₀₁、ω₀₂、ζ₀₁、ζ₀₂——将W₄(s)折成典型环节后的参数

结论：

两自由度系统的简化传递函数与单自由度系统型式相同，单自由度系统的有关结论原则上也适用于两自由度系统

项

目

分析

说明

动

态

方

程

与采用Q阀的单自由度驱动力系统相比，仅伺服阀的传递函数不同。P阀的传递函数：

K_s1——P阀的压力增益，N/(m²·A)

K_s2——P阀的流量—压力系数，N·s/m⁵

Q_V——使缸运动的强制流量，m³/s

ω_s1——P阀的一阶因子频率，rad/s

ω_s2——P阀的二阶因子频率，rad/s

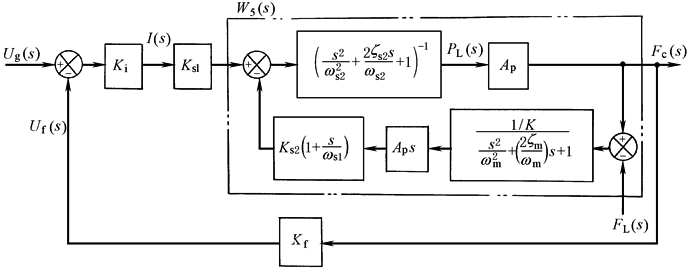
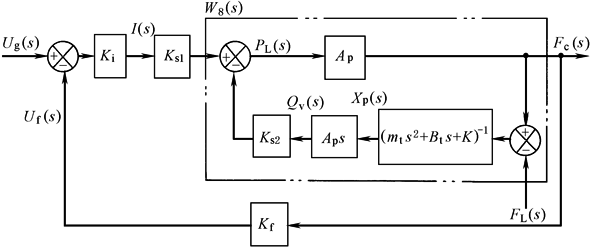
方

块

图

传

递

函

数

图中：

W₅(s)的分母为四阶，一、二项K_s2A²_ps(1+s/ω_s1)/K不会影响高阶项，因此W₅(s)可写成如下形式：

于是开环传递函数：

K_v＝K_iK_s1A_pK_f

K_v——开环增益，V/V

——机械谐振频率，rad/s

——机械阻尼系数，无因次

K——负载刚度，N/m

结论：

(1)采用P阀时，系统开环传递函数不存在采用Q阀时的二阶微分环节，也就是说采用P阀的驱动力系统的稳定性比Q阀时好得多

(2)如P阀的频宽很高，可近似看做比例环节

(3)采用P阀时，可以采用PI放大器

项目

分析

说明

动

态

方

程

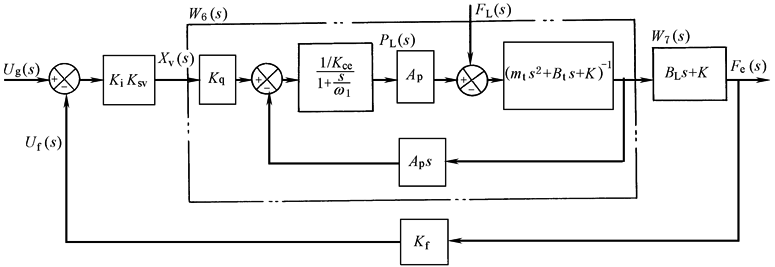
与驱动力系统相比，仅力平衡方程有所不同：

参见表电液力伺服系统的类型及特点中系统原理图

方

块

图

传

递

函

数

图中W₆(s)系以X_v(s)为输入，X_p(s)为输出的具有弹簧负载的阀控动力元件的传递函数。可直接引用表传递函数及其简化中结果，即

图中　W₇(s)＝B_Ls+K＝K(1+1/ω_b)

于是开环传递函数

K_v＝K_iK_svK_qA_pK_f/K_ce

K_v——开环增益

考虑到，且B_p=B_L，则有

于是W(s)可以简化成

如果ω₀?ω_r，则

ζ₀见表 采用Q阀的单自由度驱动力系统

ω_b＝K/B_L

结论：

(1)采用Q阀的负载力系统，不易出现采用Q阀的驱动力系统那样的严重稳定性问题

(2)可以采用PI放大器，使0型系统变成Ⅰ型系统

项

目

分析

说明

动

态

方

程

见表采用P阀的单自由度驱动力系统

为说明本质问题，设P阀的频宽很高，其传递函数可简化为

K_s1——P阀的压力增益，N/(m²·A)

K_s2——P阀的流量-压力系数，N·s/m⁵

方

块

图

传

递

函

数

图中：

于是系统开环传递函数

K'_v＝K_iK_s1A_pK_f

K'_v——开环增益，V/V

ω_m——机械谐振频率，rad/s

ζ_m——机械阻尼系数

结论：

(1)采用P阀的负载力系统，亦为0型系统

(2)对于负载力系统，看不出采用P阀有什么更为显著的好处