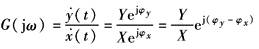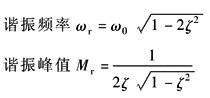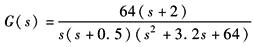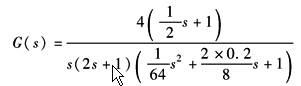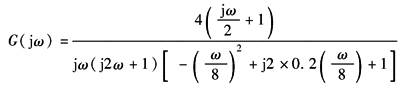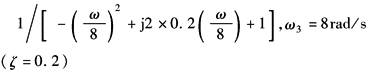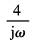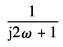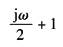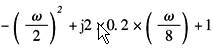线性控制系统的数学描述

定

义

线性控制系统的输入端输入正弦信号后，其输出量的稳态分量是同频率的正弦信号，但幅值和相位将随输入频率而变化。系统的频率特性就是其输出量稳态分量的复数符与输入函数复数符的比，记为G(jω)

式中　Y，X——稳态分量和输入函数的幅值；

φ_y，φ_x——稳态分量和输入函数的相位

频率特性的模等于输出稳态分量的幅值和输入函数的幅值比，称为系统的幅频特性，记为A(ω)。频率特性的幅角等于稳态分量和输入函数之间的相位差，称为系统的相频特性，记为φ(ω)。因此，频率特性是幅频特性和相频特性的统称，即

G(jω)＝A(ω)e^jφ(ω)

频率特性是线性控制系统数学模型的另一类形式，是用频率法分析和设计自动控制系统的重要工具

求

取

方

法

微分方法　以正弦函数作为系统的输入信号，求解系统输出的稳态分量，最后取二者的复数比

传递函数法　即取G(jω)＝G(s)|_s＝jω

实测方法　在系统或元件的输入端输入一定幅值且频率由小逐渐增大的正弦信号。利用频率测定仪测出对应于每一频率情况下的稳态输出和输入信号之间的幅值比和相位差。由此来确定系统或元件的频率特性

图

示

方

法

系统的频率特性通常采用下列三类图形来表示

幅相频率特性图(又称奈魁斯特图)

它是在复平面上，描绘出当频率由零变化到无限大时，G(jω)的极坐标图

对数频率特性图(又称波德图)

它是由对数幅频特性和对数相频特性两张图组成。分别绘制在半对数坐标纸上

对数幅相频率特性图(又称尼柯尔斯图)

它以频率作为参变量，在直角坐标系中绘出对数幅频特性和相位之间的关系

典

型

环

节

的

频

率

特

性

名

称

奈式图

波德图

名

称

奈式图

波德图

比

例

环

节

一

阶

微

分

环

节

微

分

环

节

积

分

环

节

惯

性

环

节

延

迟

环

节

振

荡

环

节

注：dec为十倍频程。

绘制步骤

举例

1．绘制系统的波德图

试绘制出以下系统的波德图、奈氏图和尼柯尔斯图

(1)绘制波德图时先将G(jω)改写成典型环节乘积形式

将G(s)变换成典型环节乘积形式

其频率特性为　　

(2)求出相应典型环节的转角频率

随频率的增加依次出现的典型环节和相应的转角频率ω为

比例积分环节　4/jω

惯性环节　1/(j2ω+1)，ω₁＝0.5rad/s

一阶微分环节　jω/2+1，ω₂＝2rad/s

振荡环节　

(3)随着频率的增加，以比例环节(或比例积分和比例微分环节)开始在半对数坐标纸上依次在各转角频率之间绘出相应的对数幅频特性的渐近直线

绘制相频特性时，先绘制出各典型环节的相频特性，然后根据各典型环节的相频曲线在各频率处的相位叠加，得到系统的相频特性

(4)最后通过修正渐近线得到精确的对数幅频曲线

各典型环节的对数幅频特性渐近线的特征

典型环节

ω/rad·s^-1

对数幅频渐近线特征

相频特性

无

一条斜率为-20dB/dec的直线与ω轴相交于ω＝4处

恒等于-90°

ω₁＝0.5

ω＜ω₁时为零分贝的直线

ω≥ω₁时为一条斜率为-20dB/dec的直线，交ω轴于ω＝0.5rad/s处

在0°~90°之间变化，ω＝ω₁时φ(ω₁)＝-45°

ω₂＝2

ω＜ω₂时为零分贝的直线

ω≥ω₂时为一条斜率为20dB/dec的直线，交ω轴于ω＝2rad/s处

在0°~90°之间变化，ω＝ω₂时φ(ω₂)＝45°

ω₃＝8

(ζ＝0.2)

ω＜ω₃时为零分贝的直线

ω≥ω₃时为一条斜率为-40dB/dec的直线，交ω轴于ω＝8rad/s处

在0°~-180°之间变化，ω＝ω₃时φ(ω₃)＝-90°

在半对数坐标纸上随着频率的增大，依次将上表中的典型环节的对数幅频渐近线斜率进行叠加，得到Gj(ω)的对数幅频特性渐近线。各典型环节的对数相频特性叠加，可得到系统的对数相频特性如图a

按各典型环节的对数幅频特性进行修正，可得到如图a的精确对数幅频特性^①

2．根据波德图绘制其他二图

根据波德图求取各频率下的幅值和相位，即可方便地绘制出相应的奈氏图和尼柯尔斯图，如图b和c所示

对渐近线进行幅值修正时，惯性环节和一阶微分环节可按图d求取修正量。振荡环节和二阶微分环节可按图e求取修正量。总的幅值修正量等于在各频率处修正量的代数和

根据图a可依次求出各频率值时的幅值和相位，如下

频率/rad·s^-1

0

0.5

1

2

4

7

8

10

20

∞

增益L(ω)

∞

15.3

7.3

-2.6

-8.6

-8.6

-9.3

-13

-37.3

-∞

相位φ(ω)

-90°

-123°

-127.5°

-124.5°

-127.5°

-175.5°

-196.5°

-225°

-263°

-270°

幅值A(ω)

∞

5.8

2.3

0.74

0.37

0.37

-0.34

0.22

0.14

0

o(ω)＝A(ω)cosφ(ω)

0

-3.16

-1.40

-0.42

-0.22

-0.37

-0.33

-0.16

-0.02

0

Q(ω)＝A(ω)sinφ(ω)

-∞

-4.86

-1.80

-0.60

-0.29

-0.03

0.10

0.16

0.14

0

根据上表可分别绘出系统的奈氏图b和尼柯尔斯图c

3．修正渐近线用图

①波德图可以用计算机来绘制。