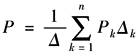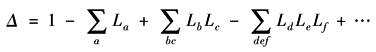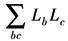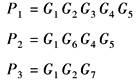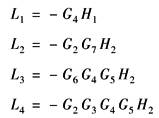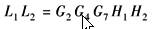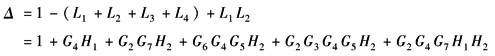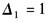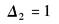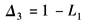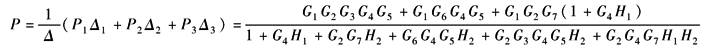线性控制系统的数学描述

定义、功能

表达形式

图中的专门术语

信

号

流

图

是另一种以图解的形式来描述控制系统中传递关系的数学图形。在控制系统的计算机模拟及状态空间分析中，利用信号流图较为方便

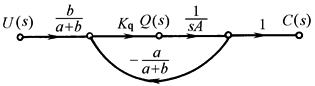
信号流图是由节点和支路所组成的信号传递网路。节点用“○”表示，它代表系统中的变量。支路是两个节点之间的定向线段，支路上的箭头表示信号的传递方向，在两变量之间的传递函数称为支路的增益。下图为表 传递函数、方块及其等次变换图c所示的液压助力器的信号流图

(1)输入节点(或源点)　只有输出支路无输入支路的节点，如左图中的U(s)

(2)输出节点(或阱点)　只有输入支路无输出支路的节点，如左图中的C(s)

(3)混合节点　既有输入支路，又有输出支路的节点，如左图中的Q(s)

(4)前向通路　从输入节点开始沿各相连支路到输出节点的通道

(5)回路　从一个节点开始又回到该节点的通道

(6)前s向通路增益　前向通路中，各支路增益的乘积

(7)回路增益　回路中各支路的增益的乘积

(8)不接触回路　没有任何公共节点的两个或两个以上回路

信

号

流

图

和

方

块

图

的

对

应

关

系

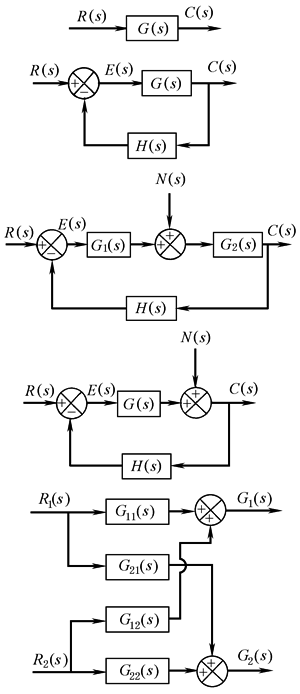
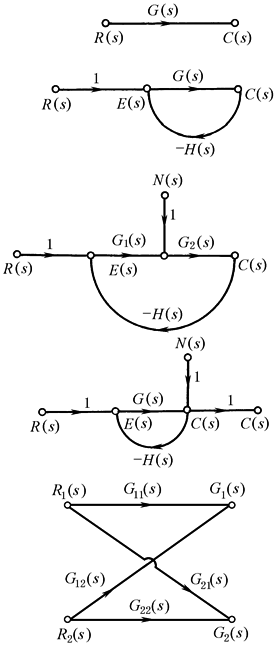
信号流图和方块图是相似的，两者一一对应。右图给出了相互对应的例子

方块图

相对应的信号流图

梅逊增益公式可用来计算输入节点和输出节点之间的总增益，即系统的传递函数。梅逊公式为

式中　P——输入节点和输出节点之间的总增益；

n——前向通路的条数；

P_k——第k条前向通路的增益；

Δ——信号流图的特征式，

——流图中每一个回路的增益之和；

——流图中每两个互不接触回路增益乘积之和；

——流图中每三个互不接触回路增益乘积之和；

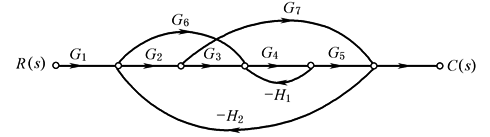
Δk——第k条前向通路特征式的余子式，它等于在Δ式中除去与第k条通路相接触的回路增益后的特征式

例　控制系统信号流图如下图所示，计算其总增益

本例中输入量为R(s)，输出量为C(s)，其间有三条前向通路。各前向通路的增益为

四个独立的回路增益为

本例中回路L₁和L₂不相接触，其他回路都相互接触。不相接触回路的增益为

流图的特征式Δ为

P₁通路中除去与其相接触的回路L₁，L₂，L₃，L₄和L₁L₂后，余子式Δ₁为

P₂通路中除去与其相接触的回路L₁，L₂，L₃，L₄和L₁L₂后，余子式Δ₂为

P₃通路中除去与其相接触的回路L₂，L₃，L₄和L₁L₂后，余子式Δ₃为

信号流图的总增益P为