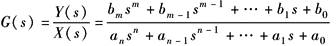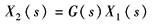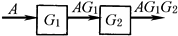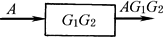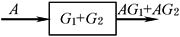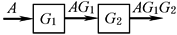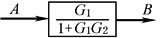传递函数及方块图
传递函数及方块图
|
传递函数、方块图及其等效变换 |
||||||||
|---|---|---|---|---|---|---|---|---|
|
传 递 函 数 |
定义及功能 |
表达(形)式 |
特点或应用 |
|||||
|
线性定常系统，在零初始条件下，其输出量的拉氏变换式和输入量的拉氏变换式之比，称为系统的传递函数，记作G(s)。它是经典控制理论中一个重要的概念，它可以用来描述元件或系统的动态特性 |
根据线性控制系统(或元件)的运动微分方程( 微分方程中式1)，在零初始条件下对等式两边逐项进行拉氏变换①，并取Y(s)和X(s)的比值，可得G(s)：
传递函数是在复变量s域内描述系统特性的数学表达式 |
(1)各项系数an、…、a0，bm、…、b0决定于系统的结构参数 (2)传递函数G(s)一般为复变量s的有理分式。其分母多项所构成的方程称为系统的特征方程。方程的根称为系统的极点。分子多项式所构成方程的根称为系统的零点 G(s)的零点、极点在复平面上的位置可以用来确定系统的稳定性和动态品质 (3)分母多项式s的阶次n，称系统的阶。由于物理条件的限制，实际控制系统分子多项式s的阶次m不可能大于分母多项式s的阶次n，即m≤n (4)传递函数的概念只适用于线性定常系统 |
||||||
|
方 块 图 |
是描述控制系统中变量之间传递关系的数学图形，是工程中描述复杂系统的一种简便方法 |
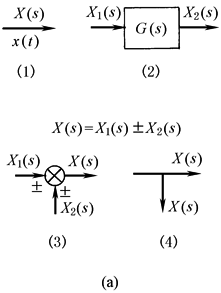
方块图的组成要素如图a所示
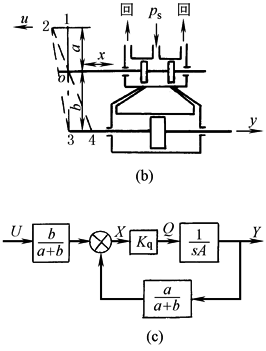
(1)信号线 带箭头的直线，箭头表示信号传递的方向，线上标注相应变量的象函数或时间函数 (2)方块 系统中的传递函数用方块来表示。方块两侧为相应的输入量和输出量，方块内写入输入与输出之间的传递函数，如图中(2)。方块具有运算功能，即
(3)比较点 对两个以上信号进行代数运算。“+”表示信号相加，“-”表示信号相减。“+”常可省略，如图中(3) (4)引出点 表示信号引出和测量的位置。从同一引出点上引出的信号，其性质和数值都是相同的，如图中(4) |
图b为液压助力器，是一种液压伺服机构
当在杠杆的1点处输入位移u时，阀芯左移使阀口开启，液压缸的活塞将向右移动并带动支点3向右移动，又使控制阀阀口减小。当支点3移动到位置4时，控制阀阀口完全关闭，液压缸活塞停止运动。反向运动时也如此。因此，通过操纵反馈连杆可以实现输入一定的位移u，将使活塞移动一定的位移y，并实现出力放大，所以该装置具有功率放大的助力作用。该系统的方块图如图c所示 该装置由控制阀、液压缸和反馈连杆三部分组成 |
|||||
|
方 块 图 的 等 效 变 换 |
即通过一定的运算法则把复杂的方块图转化成较为简单的方块图或单一方块图，以便求取系统的传递函数。等效变换的原则是变换前后系统的输入输出之间总的传递关系保持不变 |
|||||||
|
变换 方式 |
原来结构 |
等效结构 |
变换 方式 |
原来结构 |
等效结构 |
|||
|
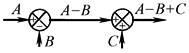
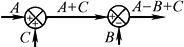
加减点互换 |
|
|
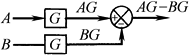
环节 串联 |
|
|
|||
|
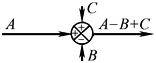
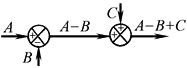
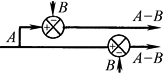
加减点重新安排 |
|
|
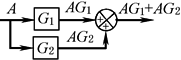
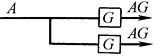
环节 并联 |
|
|
|||
|
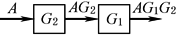
环节 互换 |
|
|
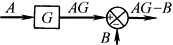
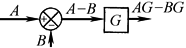
加减点左移 |
|
|
|||
|
加减点右移 |
|
|
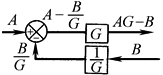
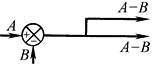
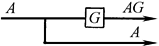
分岔点移到加减点左边 |
|
|
|||
|
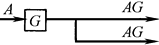
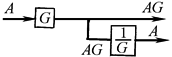
分岔点左移 |
|
|
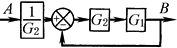
从反馈回路中移出环节 |
|
|
|||
|
分岔点右移 |
|
|
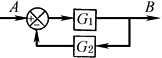
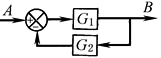
简化反馈回路 |
|
|
|||
|
①拉氏变换(拉普拉斯变换)。 |
||||||||
