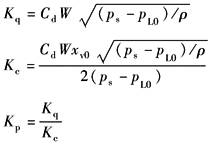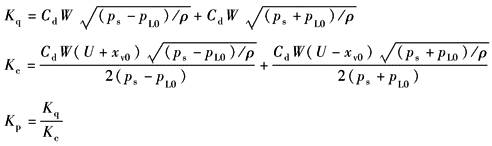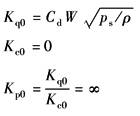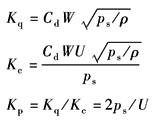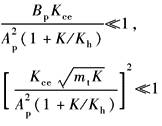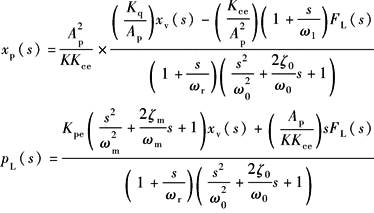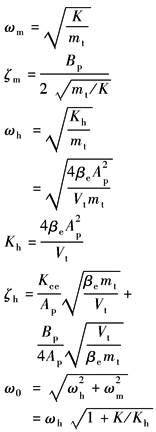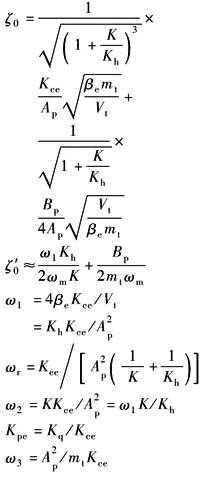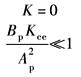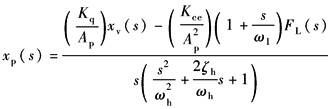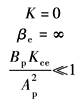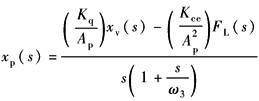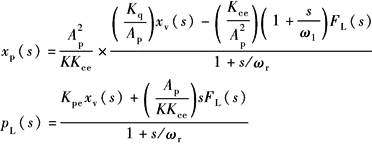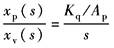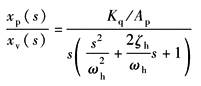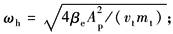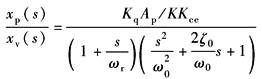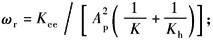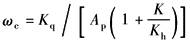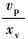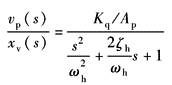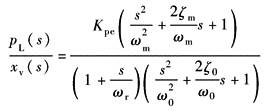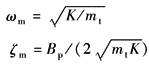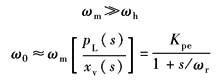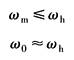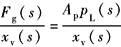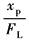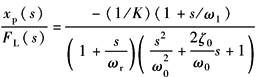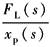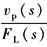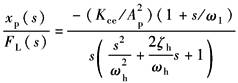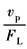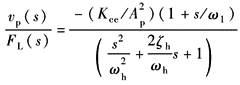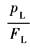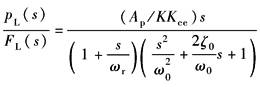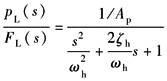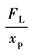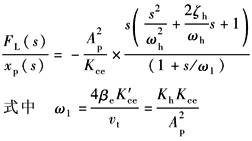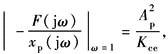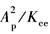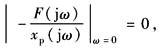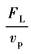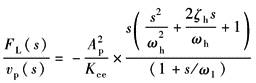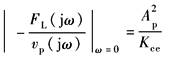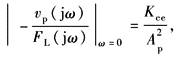液压动力元件

项目

简图及特性方程

说明

物

理

模

型

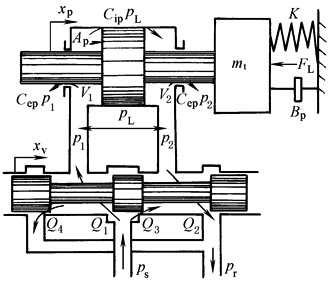
模型中滑阀为正开口阀，并假定：

(1)供油压力p_s恒定，回油压力p_r＝0；

(2)阀的四个节流窗口配作且对称，采用矩形阀口，阀口处流动为紊流；

(3)不考虑管道损失及管道的动态；

(4)温度和密度均为常数

滑阀为理想零开口阀时，Q₃＝Q₄＝0

Q_L＝(Q_ip+Q_op)/2

Q_ip＝(Q₁-Q₄)，为进入缸的流量

Q_op＝(Q₂-Q₃)，为从缸流出的流量，m³/s

s——拉普拉斯算子，1/s

K_q，K_c——工作点处的流量增益、流量-压力系数，见表 流量增益、流量-压力系数汇总

x_v——滑阀的位移，m

x_p，A_p——活塞位移、活塞工作面积，单位分别为m，m²

p_L＝(p₁-p₂)，为负载压力，N/m²

动

态

方

程

滑阀的流量方程

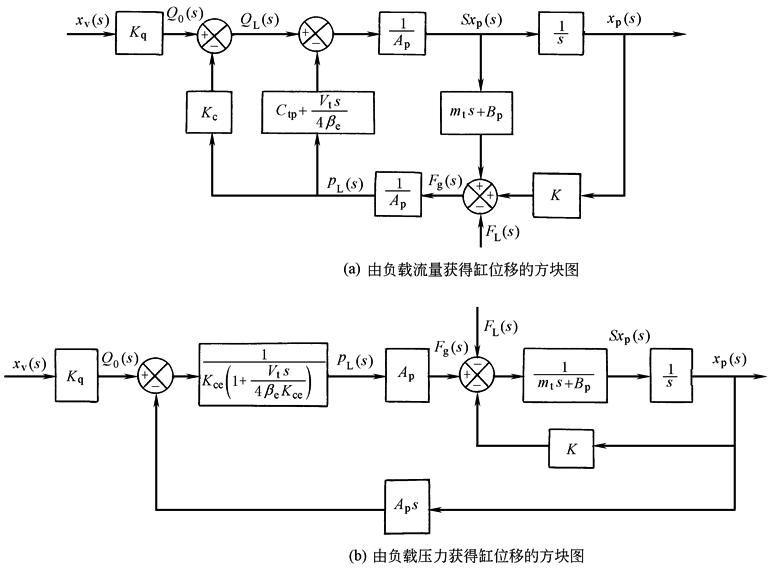
Q_L(s)＝K_qx_v(s)-K_cp_L(s)

活塞腔的连续性方程

Q_L(s)＝A_psx_p(s)+C_tpp_L(s)+(υ_t/4β_e)sp_L(s)

活塞上的力平衡方程

A_pp_L(s)＝m_ts²x_p(s)+B_psx_p(s)+Kx_p(s)+F_L(s)

方

块

图

p₁，p₂——缸两腔压力，N/m²

V_t——总容积，V_t＝(V₁+V₂)，V₁，V₂为进油腔、回油腔容积，m³

C_tp——缸的总泄漏系数，C_tp＝(C_ip+C_ep/2)，m⁵/N·s

C_ip，C_ep——缸的内、外泄漏系数，m⁵/N·s

β_e——液体的有效容积弹性模数，N/m²

m_t——活塞、油液及负载等效到活塞上的总质量，kg

B_p——活塞及负载的黏性阻尼系数，N·s/m

K——负载的弹簧刚度，N/m

K_L——作用在活塞上的外负载力，N

工作点

理想零开口四通阀

正开口四通阀

平衡点：

x_v＝x_v0

p_L＝p_L0

Q_L＝Q_L0

零点：

x_v＝0

p_L＝0

Q_L＝0

考虑因素

简化条件

简化后的传递函数

动态参数

1

质量m_t

阻尼B_p

刚度K

压缩性β_e

缸泄漏Ctp

K任意

K=K_h

K?K_h

2

质量m_t

阻尼B_p

压缩性β_e

缸泄漏C_tp

3

质量m_t

阻尼B_p

缸泄漏C_tp

4

刚度K

阻尼B_p

缸泄漏C_tp

5

空载

输出/

输入

负载

情况

传递函数及动态参数

波德图

K＝0

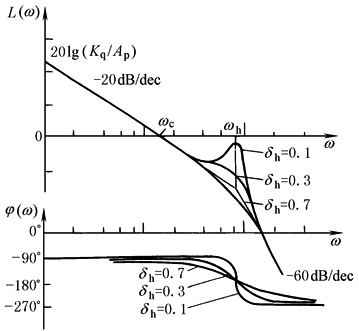
系统为Ⅰ型系统

动态参数：

(1)速度增益K_q/A_p；

(2)液压谐振频率

(3)液压阻尼系数ζ_h，见表传递函数及其简化

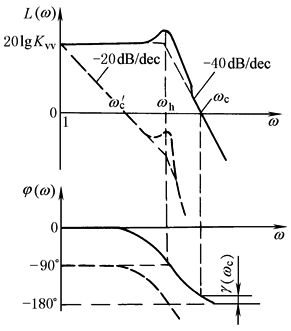
图中　L(ω)——幅频特性

φ(ω)——相频特性

ω_c——穿越频率，ω_c＝K_q/A_p

动态

特性

分析

动态特性由动态参数K_q/A_p、ω_h、ζ_h所确定：

(1)速度增益增大，则L(ω)上移、ω_c增大。意味着系统精度、响应速度提高，但稳定性变差；注意：K_q随工作点变化，零位空载时K_q最大，稳定性最差

(2)ω_h表征系统响应速度，是系统的极限频率，为提高ω_h应增大A_p、β_e而减小υ_t、m_t。通常取β_e＝700MPa；注意：空气混入系统或采用软管时，β_e大为降低

(3)ζ_h表征系统的相对稳定性，ζ_h主要取决于K_c。x_v→0时，K_c、ζ_h值最小，ζ_hmin＝0.1~0.2

K≠0

系统为0型系统，动态参数：

(1)位置增量K_qA_p/KK_ce；

(2)转折频率

(3)综合固有频率

(4)综合阻尼系数ζ₀见表传递函数及其简化

图中　穿越频率

动态

特性

分析

K≠0时，系统变成0型系统。动态特性由动态参数增益、ω_r、ω₀、ζ₀所确定

(1)动态参数均与负载刚度K有关：K增大时，增益、ω_c及ζ₀减小，而ω_r、ω₀提高，即稳态误差增大、快速性降低、超调变小

(2)注意：当K由某值变成0，即由有弹性负载转入空载时，增益由K_qA_p/KK_ce增加到K_q/A_p。瞬间增益的提高，有可能使原来稳定的系统变得不稳定。如果存在这种情况，应采取变增益控制措施

K＝0

系统为0型系统，动态参数：

(1)速度增益K_q/A_p；

(2)液压谐振频率ω_h；

(3)液压阻尼系数ζ_h

图中　虚线系加PI校正后的波德图

动态

特性

分析

(1)未加PI校正时，穿越频率ω_c处的斜率为-40dB/dec，因ζ_h很小，因此相角储备r(ω_c)很小；计及检测及伺服阀等环节造成的相位滞后以后，即使开环增益很小，闭环也可能不稳定；因此速度伺服阀系统须加PI校正

(2)采用PI校正后，穿越频率ω'_c大为降低，即动态响应降低了

K与K_h

相当

系统为0型系统

动态参数：

(1)增益K_pe＝K_q/K_ce；

(2)转折频率ω_r；

(3)综合固有频率ω₀及阻尼ζ₀；

(4)机械固有频率ω_m及阻尼ζ_m

K?K_h

K=K_h

(常见)

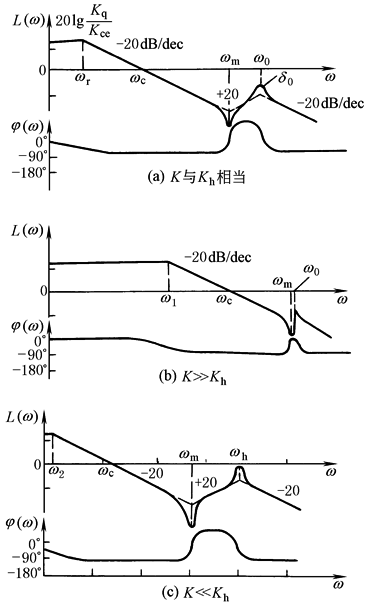
动态

特性

分析

以p_L输出时为压力控制；以驱动力F_g＝p_LA_p输出时为力控制，有。它们的特点：

(1)存在阻尼很小的二阶微分环节，且恒有ω_m＜ω₀，ω_m＝ω₀的点称为逆共振点，它是一个间断点；ω_m是力控制系统频宽的极限值；ω＞ω_m易出现自激振荡，为不可用域

(2)为提高系统频宽，应设法增大ω_c，为此应增大K_q、减小A_p；力及压力系统中，在保证驱动力的前提下，通过减小A_p来提高系统频宽，这一点是与位置及速度控制中不同的

输出/

输入

负载

情况

传递函数

频率特性

动态特性分析

K≠0

(动态位置柔度特性)

与分析x_v作用下的频率特性一样，原则上可对F_L作用下的频率特性进行类似的分析

在F_L作用下，更关心的是：

(1)动态位置刚度特性(对位置控制)

(2)动态速降特性(对速度控制)

K＝0

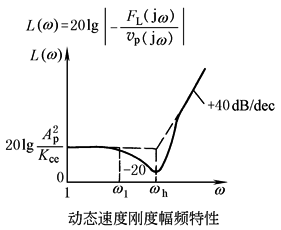
K＝0

(动态速度柔度特性)

K≠0

K＝0

K＝0

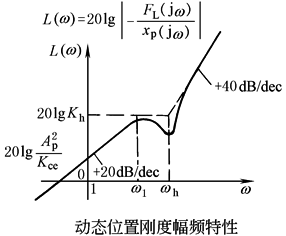
动态位置刚度特性的物理解释如下

(1)ω＜ω₁的低频段：渐进线斜率为+20dB/dec，当ω＝1时，正是稳态

速度刚度，说明低频时阀控缸相当于一个

阻尼系数为的黏性阻尼器，阻尼

作用相当于泄漏流量通道所造成的结果

(2)ω₁＜ω＜ω_h的中频段：渐进线斜率为0，由于外负载力的变化频率高，没有足够的时间让泄漏流量通过，油液被封在缸的两腔，因而动态刚度等于K_h

(3)ω＞ω_h的高频段，渐进线斜率为+40dB/dec，由于F_L的变化频率极高，快速“退让”运动产生很大的惯性力，抵消了F_L的作用，因而动态刚度呈二次幂增加

(4)ω＝0的刚度为稳态位置刚度，其值为这是由于F_L作

用下泄漏，使活塞不断后退，因而稳态位置刚度为零

K＝0

(1)ω＝0时的稳态速度刚度：

(2)反之，稳态速度柔度：

其含义为

外负载力要引起速降

由于K_ce很小，稳态速度柔度很小，这正是液压伺服系统的特点，是液压伺服系统得到广泛应用