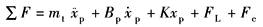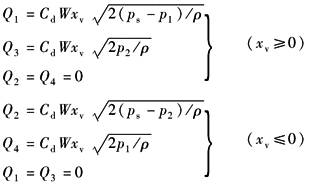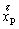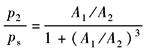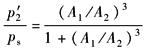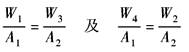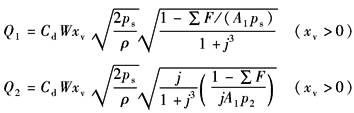液压动力元件

项

目

内容

说明

物

理

模

型

(a)对称四通阀控制不对称缸简图

假设：缸为单活塞杆不对称缸，阀为对称的零开口四通阀

图中　A₁，A₂——无杆腔、有杆腔工作面积，m²

p₁，p₂——无杆腔、有杆腔工作压力，MPa

∑F——总负载，N

∑F₁——x_p＞0时的总负载

∑F₂——x_p＜0时的总负载

F_L，F_c——外负载力、摩擦力

B_p——黏性阻尼系数，N·s/m

x_v，x_p——滑阀、活塞位移，m

V₁，V₂——无杆腔、有杆腔容积，m³

Q₁~Q₄——通过阀口1~4的流量，m³/s

动

态

方

程

阀

的

流

量

方

程

连

续

性

方

程

数字仿真：由于缸的不对称，难以获得系统的传递函数及频率特性，必须根据动态方程组，通过数字仿真求出系统的动态特性

活

塞

运

动

方

程

压

力

及

压

力

跃

变

有

负

载

时

为简化分析，分析压力跃变时，未考虑油的压缩性和缸的泄漏情况

式中　p₁，p₂——＞0时V₁、V₂腔内的压力

p'₁，p'₂——＜0时V₁、V₂腔内的压力

Δp₁，Δp₂——V₁，V₂腔内的压力跃变值

——p₁，p₂对时间的微分

空

载

时

运动状况

压力关系

A₁/A₂＝1

A₁/A₂＝1.71

A₁/A₂＝2

0.500

0.167

0.111

0.500

0.285

0.222

0.500

0.487

0.444

0.500

0.833

0.889

附近压力跃变

Δp₁＝p₁-p'₁

0

0.320p_s

0.333p_s

Δp₂＝p₂-p'₂

0

0.548p_s

0.667p_s

结

论

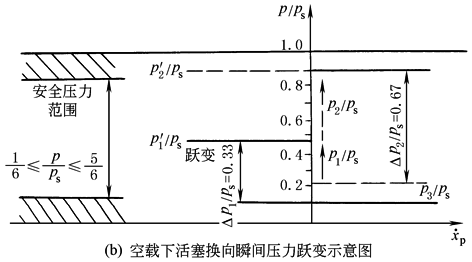
(1)只要A₁/A₂≠1，即只要对称四通阀控制的是不对称缸，在运动的换向瞬间，即＝0附近，便要出现巨大的压力跃变

(2)表中数据是假定空载且不考虑油液的压缩性条件下得到的，如考虑负载和油液的压缩性，则压力跃变值将大于表中的数值

(3)缸内工作压力的变化范围为0＜p＜p_s，为留有安全裕量，要求(1/6)p_s≤p≤(5/6)p_s。但当A₁/A₂＞1.71时，即使在空载条件下，缸内工作压力(p₁或p₂)也超出(1/6)p_s≤p≤(5/6)p_s的范围

(4)由于存在油液的压缩性，因此，在巨大的压力跃变下，必引起油液的“内爆”或“外爆”，由此即使在＝0附近，也不可能平稳地工作

(5)对于要求精确且平稳的控制场合，对称四通阀同不对称缸的不相容性是显然的，为了避免压力的跃变并确保能平稳地工作，必须采取有效的措施

(6)表中数据是假定∑F₁＝∑F₂＝0的空载情况下得到的。如果∑F₁＝∑F₂为恒定载荷，将使p₁、p₂偏置一定值，但压力跃变的幅值不变。实际工作中载荷并非常量，压力的偏置值和压力跃变幅值都将随工况而变化，即随运动状态和负载而变化

方法名称

方法及原理

实质及特点

1.阀口面积补偿法

由表动态方程及压力跃变中图a，并令L₁＝L₂＝L/2，可导出平稳控制的条件：

式中，W₁、W₂、W₃、W₄分别为阀口1、2、3、4的面积梯度

实质是采用不对称阀，利用阀的面积梯度与活塞面积进行匹配、补偿

特点是必须采用非标准伺服阀，L₁≠L₂≠L/2时结果是近似的

2.非线性算法或电路补偿法

(1)由表动态方程及压力跃变中图a，不计油的压缩性及缸的泄漏，并令j＝A₂/A₁，可导出补偿前流量公式：

式中，x_v＝K_xI，I为伺服阀的输入电流

(2)活塞杆上装一只拉压力传感器检测∑F

(3)作两个非线性函数或电路

(4)按左图算法及接法，并加方向鉴别器，可得补偿后Q₁、Q₂的等效流量

非线性补偿的算法或电路接法

该补偿法的实质是通过算法或电路产生补偿电流，使阀产生补偿位移，以补偿面积差，该补偿法对活塞任意位置均适用，但因未计及油的压缩性，故属静态补偿