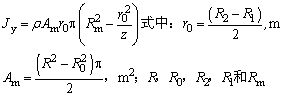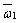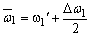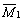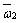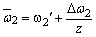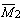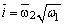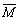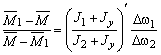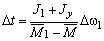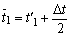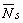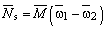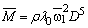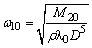液力偶合器

对于某些要求频繁启动的大惯量工作机，例如离心分离机，启动、停车等过渡过程时间占装置总使用时间达很大的比例，有时需要计算启动过程中各参数随启动时间的变化关系。图(1)为带偶合器传动系统原理图。

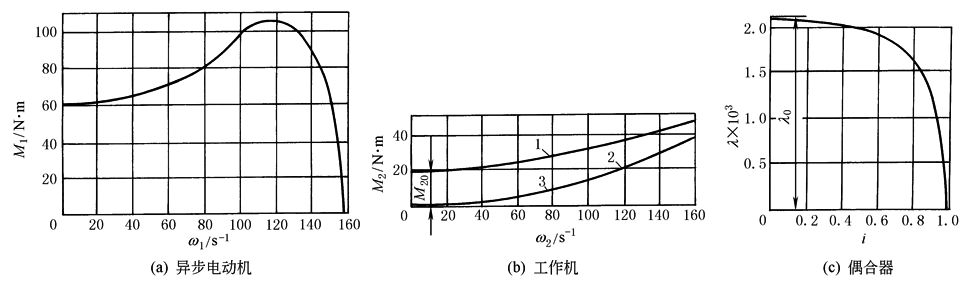
图(1)　带偶合器传动系统原理图

1—异步电动机；2—工作机；J₁—系统主动部分，包括电动机、偶合器泵轮，转动外壳等转算到偶合器输入轴上的转动惯量；

J₂—系统从动部分转动惯量，包括涡轮，转算到偶合器输出轴上；ω₁和M₁—电动机角速度和转矩；

ω₂和M₂—工作机的角速度和转矩；M—偶合器所传转矩；J_y—偶合器中液体相对于旋转轴的转动惯量

在计算启动特性之前，必须具有该传动系统的异步电动机的负荷特性M₁＝M₁(ω₁)；工作机的负荷特性M₂＝M₂(ω₂)和偶合器的无因次特性λ＝f(i)，见图(2)。并假定在启动特性计算中可利用上述三者的静态转矩特性。

图(2)　某带偶合器传动系统的一些原始特性

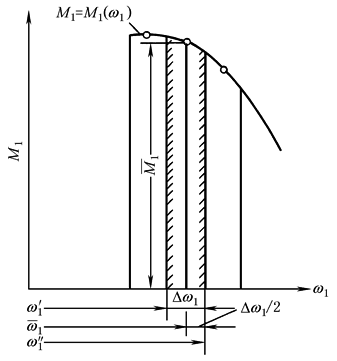
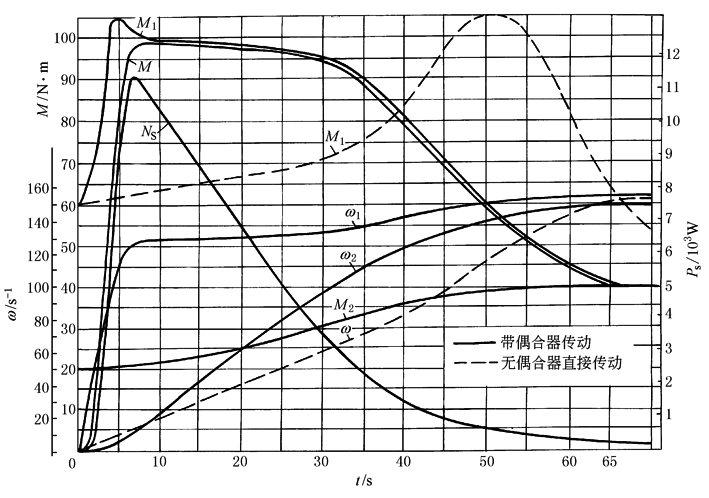
图(3)　电动机负荷特性

图中计算的参数为：J₁＝20kg·m²，J₂＝200kg·m²；D＝0.2m，ρ＝900kg/m³；异步电动机负荷特性为图(2)a，工作机负荷特性为图(2)b中的曲线1，偶合器无因次特性为图(2)c，图(4)中还与异步电动机直接带动工作机(无偶合器)的启动特性作了比较。可以看出，在本例情况下，带偶合器的传动系统，在5s后电动机即可越过最大转矩，65s已达到稳定运转工况；对于不带偶合器的，越过电动机最大转矩的时间为52s，达到稳定运转工况则需更长的时间。

图(4)　某偶合器传动系统启动特性的计算结果

带偶合器传动系统启动特性计算

序 列

参  数

计算公式或来源

1

主动部分的转动惯量(转算到偶合器输入轴上)J₁/kg·m²

根据系统的具体情况，按动力学基本公式计算

2

从动部分的转动惯量(转算到偶合器输出轴上)J₂/kg·m²

根据工作机和偶合器具体情况，按动力学基本公式计算

3

偶合器叶轮内液体对旋转轴的转动惯量J_y/kg·m²

的含义与计算公式，见表“轴向推力计算”；ρ——工作油密度，kg/m³

4

某一步长的计算初始值t₁'/s；ω₁'/s^-1；ω₂'/s^-1

对传动系统由静止开始启动的，取t₁'＝0，ω₁'＝0，ω₂'＝0。如非静止开始启动，则取另外值。t₁'，ω₁'和ω₂′——某步长起始瞬间的时间，主动部分角速度和从动部分角速度

5

经过很小时间间隔△t之后电动机的角速度增量△ω₁/s^-1

根据具体情况取定。取得小，计算精度高，计算量大；取得大，精度低，计算量少

6

电动机的平均角速度/s^-1

7

与对应的电动机平均转矩/N·m

由电动机负荷特性M₁＝M₁(ω₁)查得。见图(3)

8

经过很小时间间隔△t之后工作机的角速度增量△ω₂/s^-1

根据具体情况先取定，经校核后再修正，逐次接近

9

工作机的平均角速度/s^-1

10

与对应的工作机平均转矩/N·m

由工作机负荷特性M₂＝M₂(ω₂)查得。与图(3)所示方法类似

11

偶合器平均转速比

12

与对应的偶合器转矩系数

由所用偶合器无因次特性λ＝f(i)查得

13

与对应的偶合器所传的平均转矩，N·m

14

校核传动系统的运动微分方程式

等式两边必须相等，如不等，重新取△ω₂，重复序列8到13计算，到满意的相等为止。再往下计算

15

对应该步长的时间间隔△t/s

16

平均时间/s

17

该步长的终点参数t₁"/s；ω₁"/s^-1；ω₂"/s^-1

t₁"＝ t₁'+△t

ω₁"＝ω₁'+△ω₁

ω₂"＝ω₂'+△ω₂

作为下一个步长计算的初始值

18

该时间间隔内偶合器的功率损失/kW

注：1.序列4到18为第一个时间间隔的计算结果，之后，以t₁"，ω₁"和ω₂"作为初始值，重复由4到18，算出第二时间间隔各参数。再重复上述算法，直到启动过程结束，传动系统稳定运转为止。最后作出、、、、和随的变化关系曲线图(见图(4))。

2.如果工作机的起始转矩(ω₂＝0时的M₂₀)不等于零(图(2)b中的曲线1和2)，则在工作机转动之前，ω₂'，和均等于零，(λ₀为i＝0时偶合器转矩系数)，可按上表算出工作机转动之间的、、、和。与此价段终了时相应的电动机角速度。

3.据＝f()的关系曲线，可以标出整个启动过程中转换成热量的功A_s＝∑·△t(W·s)。